
- Investment
- 科学论坛
-
Program
News Message
信号与系统
- by wittx 2022-06-24
信号与系统
- 绪论
- 1.1 绪言
- 信号:消息的表现形式与传送载体
- 系统:由若干相互作用和相互依赖的事物组合而成的,具有稳定功能的整体
- 信号理论:信号分析、信号传输、信号处理、信号综合
- 系统理论:系统分析、系统综合
- 1.2 信号的描述、分类和典型示例
- 信号的分类
- 确定性or随机
- 周期or非周期
- 连续or离散
- 模拟信号(时间幅值都连续)、抽样信号(时间离散、幅值连续)、数字信号(时间幅值均离散)
- 几种典型确定性信号
- 指数信号:其对时间的微分和积分仍然是指数形式
- 正弦信号
- 复指数信号:欧拉公式
![[公式]](/images/download/1656037190983_24939.png)
![[公式]](/images/download/1656037191593_82683.png) 为复数,称为复频率
为复数,称为复频率- 抽样信号
![[公式]](/images/download/1656037191730_19496.png)
抽样信号(作图软件:Origin) 性质:偶函数,
![[公式]](/images/download/1656037191971_71483.png)
- 钟形脉冲函数(高斯函数)
![[公式]](/images/download/1656037192133_77201.png)
钟形脉冲函数(作图软件:Matlab) - 1.3 信号的运算
- 信号的自变量的变换(波形变换)
- 平移
- 反转
- 尺度变换
- 一般情况
![[公式]](/images/download/1656037192330_26578.png) (设a>0)
(设a>0) - 微分和积分
- 两信号相加或相乘
- 1.4 阶跃函数和冲激函数
奇异函数:本身或导数或积分不连续 - 单位斜变信号
- 单位阶跃信号
- 门函数(窗函数)
![[公式]](/images/download/1656037192518_74686.png)
门函数(作图软件:Matlab) - 符号函数
![[公式]](/images/download/1656037192725_29964.png)
符号函数(作图软件:Matlab) - 单位冲激信号
- 定义1:函数值只在0时不为零;积分面积为1;t=0无界
- 定义2:(若面积为k,则强度为k;三角形脉冲、双边指数脉冲、钟形脉冲、抽样函数取t→0极限)
![[公式]](/images/download/1656037192963_83342.png)
- 冲激函数的性质
- 抽样性
![[公式]](/images/download/1656037193132_49444.png)
![[公式]](/images/download/1656037193355_85694.png)
- 奇偶性
n为偶数:
![[公式]](/images/download/1656037193633_76369.png) 为偶函数;n为奇数:
为偶函数;n为奇数: ![[公式]](/images/download/1656037193857_59246.png) 为奇函数;
为奇函数;- 标度变换
![[公式]](/images/download/1656037194012_43660.png)
- 卷积性质
![[公式]](/images/download/1656037194143_89431.png)
- 冲激偶信号
- 面积为1的函数求导了再取极限
- 性质
![[公式]](/images/download/1656037194289_16764.png)
![[公式]](/images/download/1656037194528_39617.png)
![[公式]](/images/download/1656037194683_73599.png) (奇函数)
(奇函数)![[公式]](/images/download/1656037194822_85880.png)
- 标度变换
![[公式]](/images/download/1656037194974_76625.png) ,
, ![[公式]](/images/download/1656037195141_42213.png)
- 1.5 系统的描述
- 描述系统的基本单元方框图:加法器、乘法器、标量乘法器(数乘器,比例器)、微分器、积分器、延时器
- 系统的定义和表示
- 定义:具有特定功能的总体,可以看作信号的变换器、处理器
- 表示
- 数学表达式:系统物理特性的数学抽象
- 系统框图:形象地表示其功能
- 系统的分类
- 连续时间系统:微分方程;离散时间系统:差分方程、混合系统
- 即时系统(非记忆系统):代数方程;动态系统(记忆系统):微分方程或差分方程
- 集总参数系统:常微分方程(t);分布参数系统:偏微分方程(t,x,y,z)
- 线性or非线性
- 时变or时不变
- 因果or非因果
- 可逆or不可逆
- 1.6 系统的特性和分析方法
- 线性系统与非线性系统
- 齐次性、叠加性
- 判断方法:先线性运算,再经系统=先经系统,再线性运算,则为线性
- 时变系统与时不变系统
- 先时移,再经系统=先经系统,再时移,则时不变
- 线性时不变系统的微分特性、积分特性
- 因果系统与非因果系统
- 判断方法:输出不超前于输入,则为因果系统
- 实际的物理可实现系统均为因果系统
- 因果信号:t= 0接入系统的信号
- 建立系统模型的两种方法(最后一章还会提及)
- 输入——输出描述法
- 着眼于激励与响应的关系,而不考虑系统内部变量情况
- 单输入/单输出系统
- 列写一元n阶微分方程
- 状态变量分析法
- 不仅可以给出系统的响应,还可以描述内部变量,如电容电压或电感电流的变化情况
- 研究多输入/多输出系统
- 列写多个一阶微分方程
- 数学模型的求解方法
- 时域分析:经典&卷积
- 变换域分析:傅里叶、s、z等
- 连续时间系统的时域分析
- 列写方程:系统数学模型(微分方程)的建立
- 主要是根据元件特性约束和网络拓扑约束建立
- n 阶线性时不变系统的描述(方程的阶次由独立的动态元件的个数决定)
![[公式]](/images/download/1656037195328_90749.png)
![[公式]](/images/download/1656037195503_35161.png)
若系统为时不变,则C,E均为常数,此方程为常系数的n阶线性常微分方程
- 解方程的方法
- 经典法:全解(全响应)=齐次解(自由响应)+特解(强迫响应)
- 全响应=零输入响应+零状态响应
- 零输入(激励为0,起始状态不为0):可以利用经典法求解
![[公式]](/images/download/1656037195844_64535.png)
- 零状态(起始状态为0,激励不为0):利用卷积积分法求解
![[公式]](/images/download/1656037195970_24850.png)
- 线性系统响应的分解:补充一种分解——全响应=暂态响应+稳态响应
- 对系统线性的进一步认识:由常系数微分方程描述的系统,若能分解为零输入+零状态,且零输入线性、零状态线性,则系统线性
- 变换域法(下一章)
- 冲激响应和阶跃响应
- 起始点的跳变
- 0-状态:起始状态
- 0+状态:初始条件、导出的起始状态
- 电容电压的突变:有冲激电流或阶跃电压作用于电容
- 电感电流的突变:有冲激电压或阶跃电流作用于电感
- 当系统用微分方程表示时,系统从0-到 0+状态有没有跳变取决于微分方程右端自由项是否包含冲激函数及其各阶导数项
- 冲激响应
- 在单位冲激信号作用下产生的零状态响应,称为单位冲激响应,简称冲激响应,一般用h(t)表示
- 冲激在t=0时转为系统的储能(由vc(0+)体现),t>0时,在非零初始条件下齐次方程的解,即为原系统的冲激响应
- 奇异函数项相平衡法:把特征方程系数未知的解代入原方程求系数
- n阶系统的冲激响应
- 冲激响应的数学模型
![[公式]](/images/download/1656037196134_60904.png)
![[公式]](/images/download/1656037196294_47574.png)
- h(t)解答的形式——自由项恒等于零,冲激响应形式与齐次解的形式相同
①与特征根有关,设特征根为简单根(无重根的单根)
![[公式]](/images/download/1656037196481_44880.png)
②与n,m相对大小有关:n>m,
![[公式]](/images/download/1656037196722_92303.png) 不含
不含![[公式]](/images/download/1656037196844_20516.png) 及其各阶导数;n=m,
及其各阶导数;n=m,![[公式]](/images/download/1656037196969_56471.png) 含
含![[公式]](/images/download/1656037197104_49641.png) ;n<m,
;n<m,![[公式]](/images/download/1656037197259_59244.png) 含
含![[公式]](/images/download/1656037197485_73594.png) 及其各阶导数;
及其各阶导数;- 齐次解法求冲激响应
解方程:
![[公式]](/images/download/1656037197613_15197.png)
其中
![[公式]](/images/download/1656037197820_68214.png)
![[公式]](/images/download/1656037197987_20677.png) 即为
即为 ![[公式]](/images/download/1656037198115_50324.png) 的线性组合。
的线性组合。- 阶跃响应
- 阶跃响应与冲激响应的关系(阶跃响应是冲激响应的积分,可用于求解)
- 卷积积分
- 卷积
![[公式]](/images/download/1656037198254_26317.png) ,记为
,记为 ![[公式]](/images/download/1656037198395_54152.png) 或
或 ![[公式]](/images/download/1656037198581_65913.png)
- 利用卷积积分求系统的零状态响应
任意信号f(t)可表示为冲激序列之和
![[公式]](/images/download/1656037198713_32881.png)
若把它作用于冲激响应为h(t)的LTIS,则响应为
![[公式]](/images/download/1656037198846_60106.png)
即系统的零状态响应
![[公式]](/images/download/1656037199006_18788.png)
- 卷积图解说明
- 卷积积分的几点认识
- 卷积积分的性质
- 卷积的代数运算
交换律
![[公式]](/images/download/1656037199156_12317.png)
分配律(系统并联)
![[公式]](/images/download/1656037199313_19336.png)
结合律(系统级联)
![[公式]](/images/download/1656037199475_18545.png)
- 卷积的微分与积分
![[公式]](/images/download/1656037199685_31459.png)
推广 :
![[公式]](/images/download/1656037199916_63917.png)
- 函数与冲激函数的卷积
![[公式]](/images/download/1656037200121_31401.png)
推广:
![[公式]](/images/download/1656037200304_99625.png)
![[公式]](/images/download/1656037200473_98673.png)
![[公式]](/images/download/1656037200726_48753.png)
- 傅里叶变换
- 由时域转入变换域分析
- 信号的分解(正交分解)
- 周期信号的傅里叶级数分析(满足狄里赫利条件)
- 三角函数形式的傅立叶级数
![[公式]](/images/download/1656037200873_54437.png)
傅里叶系数:
![[公式]](/images/download/1656037201117_18713.png)
![[公式]](/images/download/1656037201305_83064.png)
- 指数形式的傅里叶级数(欧拉公式推出)
![[公式]](/images/download/1656037201479_59036.png)
系数
![[公式]](/images/download/1656037201775_40608.png)
- 周期信号的对称性与傅里叶系数的关系
- 偶函数:傅里叶级数中不含正弦项;Fn=F(nw1)为实函数
- 奇函数:傅里叶级数中不含余弦项;Fn=F(nw1)为虚函数
- 奇谐函数
![[公式]](/images/download/1656037202078_81868.png) ,f(t)的傅氏级数偶次谐波为零
,f(t)的傅氏级数偶次谐波为零 - 偶谐函数
- 频谱(频率分量的组成如何?)
- 幅度频谱:单边幅度谱、双边幅度谱
- 相位频谱:单边相位谱、双边相位谱
- 注:当Fn为实数(偶函数),那么相位频谱可用Fn的正负来表示,相位为0或Pi,这时常把幅度谱和相位谱画在一张图上
- 周期信号的功率
![[公式]](/images/download/1656037202274_51160.png) (帕塞瓦尔( Parseval)定理)
(帕塞瓦尔( Parseval)定理) - 傅里叶有限级数与最小方均误差
- 典型周期信号的傅里叶级数
- 周期矩形频谱结构
- 周期矩形
- 三角函数形式的谱系数:偶函数,无正弦项
- 指数函数形式的谱系数
![[公式]](/images/download/1656037202456_91695.png)
- 抽样信号频谱特点(Fn是实函数,可合并)
- 周期信号频谱的特点:离散性、谐波性、收敛性
- 频带宽度:信号的功率集中在低频段;系统的通频带>信号的带宽,才能不失真
一般把第一个零点作为信号的频带宽度。记为:
![[公式]](/images/download/1656037202625_58381.png) 或
或 ![[公式]](/images/download/1656037202769_57839.png) (带宽与脉宽成反比);对于一般周期信号,将幅度下降为
(带宽与脉宽成反比);对于一般周期信号,将幅度下降为 ![[公式]](/images/download/1656037202994_50692.png) 的频率区间定义为频带宽度
的频率区间定义为频带宽度- 傅里叶变换
- 傅里叶变换
![[公式]](/images/download/1656037203140_62279.png)
频谱密度函数
![[公式]](/images/download/1656037203284_17611.png) 一般为复信号:
一般为复信号: ![[公式]](/images/download/1656037203439_98493.png)
- 傅里叶反变换
当
![[公式]](/images/download/1656037203588_84037.png) 时,
时, ![[公式]](/images/download/1656037203733_24239.png) ,
, ![[公式]](/images/download/1656037203877_63173.png)
- 傅里叶变换对
![[公式]](/images/download/1656037204015_22224.png)
简写
![[公式]](/images/download/1656037204307_41260.png)
- 傅里叶变换的物理意义
- 无穷多个振幅为无穷小的连续余弦信号之和,频域范围:0→∞
- 无穷多个幅度为无穷小的连续指数信号之和,占据整个频域
- 傅里叶变换存在的条件:
![[公式]](/images/download/1656037204783_60792.png) 绝对可积
绝对可积 - 典型非周期信号的傅里叶变换
- 矩形脉冲
- 单边指数信号
- 直流信号
![[公式]](/images/download/1656037205058_78894.png)
- 符号函数
![[公式]](/images/download/1656037205190_60224.png)
- 升余弦脉冲信号
![[公式]](/images/download/1656037205336_62528.png)
- 冲激函数→直流
- 阶跃函数
![[公式]](/images/download/1656037205519_91772.png)
- 傅里叶变换的基本性质
- 线性性质
- 奇偶虚实性
![[公式]](/images/download/1656037205677_41492.png) ,其中
,其中 ![[公式]](/images/download/1656037205823_16886.png) 是偶分量,
是偶分量, ![[公式]](/images/download/1656037205944_79686.png) 是奇分量
是奇分量![[公式]](/images/download/1656037206084_23250.png)
可以命名函数:
![[公式]](/images/download/1656037206291_78896.png) 是关于
是关于 ![[公式]](/images/download/1656037206436_73623.png) 的偶函数,
的偶函数, ![[公式]](/images/download/1656037206557_63213.png) 是关于
是关于 ![[公式]](/images/download/1656037206739_75252.png) 的奇函数
的奇函数则
![[公式]](/images/download/1656037207153_19549.png) 的幅值函数
的幅值函数![[公式]](/images/download/1656037207286_42494.png) ,相位函数
,相位函数 ![[公式]](/images/download/1656037208284_15738.png)
可得到结论:
![[公式]](/images/download/1656037208418_29671.png) 为偶函数
为偶函数 ![[公式]](/images/download/1656037208554_46934.png)
![[公式]](/images/download/1656037208694_26070.png) 为实函数,只有
为实函数,只有 ![[公式]](/images/download/1656037208865_49989.png) ,相位
,相位 ![[公式]](/images/download/1656037209003_11126.png)
![[公式]](/images/download/1656037209147_55825.png) 为奇函数
为奇函数 ![[公式]](/images/download/1656037209277_11559.png)
![[公式]](/images/download/1656037209412_33453.png) 为虚函数,只有
为虚函数,只有 ![[公式]](/images/download/1656037209528_87295.png) ,相位
,相位 ![[公式]](/images/download/1656037209728_76125.png)
- 对称性质
若
![[公式]](/images/download/1656037209855_30867.png) ,则
,则 ![[公式]](/images/download/1656037210060_93686.png)
若
![[公式]](/images/download/1656037210195_37152.png) 为偶函数,则
为偶函数,则 ![[公式]](/images/download/1656037210322_45727.png)
- 尺度变换性质
若
![[公式]](/images/download/1656037210441_81035.png) ,则
,则 ![[公式]](/images/download/1656037210577_26525.png) ,a非零
,a非零- 信号的持续时间与信号占有频带成反比
- a=-1时,
![[公式]](/images/download/1656037210769_99310.png)
- 时移特性
若
![[公式]](/images/download/1656037211116_25463.png) ,则
,则 ![[公式]](/images/download/1656037211257_66772.png)
- 频移特性:可用于调制与解调,频分复用
若
![[公式]](/images/download/1656037211409_49941.png) ,则
,则 ![[公式]](/images/download/1656037211551_72362.png) ,
, ![[公式]](/images/download/1656037211688_42360.png) 为常数
为常数- 微分特性
时域微分性质
![[公式]](/images/download/1656037211887_19114.png)
频域微分性质
![[公式]](/images/download/1656037212064_88365.png)
- 积分特性
![[公式]](/images/download/1656037212208_16624.png)
- 时域卷积定理
![[公式]](/images/download/1656037212353_60988.png)
- 频域卷积定理
![[公式]](/images/download/1656037212568_29444.png)
- 卷积定理应用
①用时域卷积定理求频谱密度函数
②求
![[公式]](/images/download/1656037212719_69766.png) 的傅里叶变换
的傅里叶变换③求系统的响应
- 周期信号的傅里叶变换
- 正弦信号的傅里叶变换
![[公式]](/images/download/1656037212841_32022.png)
![[公式]](/images/download/1656037213060_76508.png)
- 一般周期信号的傅里叶变换
![[公式]](/images/download/1656037213316_56050.png)
- 周期单位冲激序列的傅里叶变换及其对比
- 周期矩形脉冲序列的傅氏变换
- 脉冲序列的傅里叶系数F(nw1)与单脉冲傅里叶变换F0(w)的关系
![[公式]](/images/download/1656037213508_39969.png)
- 抽样型号的傅里叶变换
- 取样:从连续时间信号中抽取一系列离散样本值的过程
- 冲激抽样信号的频谱
- 抽样定理
一个频带受限的信号
![[公式]](/images/download/1656037213681_31221.png) ,若频谱只占据
,若频谱只占据 ![[公式]](/images/download/1656037213809_21026.png) 的范围,则信号可用等间隔的抽样值来唯一表示,其抽样间隔必须不大于
的范围,则信号可用等间隔的抽样值来唯一表示,其抽样间隔必须不大于 ![[公式]](/images/download/1656037213944_38061.png) ,即(奈奎斯特抽样间隔 )
,即(奈奎斯特抽样间隔 )![[公式]](/images/download/1656037214065_78485.png) ,或者说最低抽样频率为(奈奎斯特抽样频率)
,或者说最低抽样频率为(奈奎斯特抽样频率) ![[公式]](/images/download/1656037214198_70466.png)
- 拉普拉斯变换、连续时间系统的s域分析
- 拉普拉斯变换的定义、收敛域
- 拉普拉斯正变换
![[公式]](/images/download/1656037214328_38872.png)
- 拉氏逆变换
![[公式]](/images/download/1656037214555_75153.png)
- 考虑到实际信号都是有起因信号
采用0-系统,相应的单边拉氏变换为
![[公式]](/images/download/1656037214715_56102.png)
- 拉氏变换的收敛
![[公式]](/images/download/1656037214918_51863.png)
- 一些常用函数的拉氏变换
- 拉普拉斯变换的基本性质
- 线性
- 延时(时域平移)
若
![[公式]](/images/download/1656037215060_54083.png) ,则
,则 ![[公式]](/images/download/1656037215396_90959.png)
- s域平移
若
![[公式]](/images/download/1656037215577_79398.png) ,则
,则 ![[公式]](/images/download/1656037215718_92760.png)
- 尺度变换
若
![[公式]](/images/download/1656037216142_56164.png) ,则
,则 ![[公式]](/images/download/1656037216391_78706.png)
- 原函数微分
若
![[公式]](/images/download/1656037216540_53355.png) ,则
,则 ![[公式]](/images/download/1656037216679_43132.png)
- 电感元件的s域模型
- 原函数的积分
若
![[公式]](/images/download/1656037216939_41569.png) ,则
,则 ![[公式]](/images/download/1656037217238_81860.png)
- 电容元件的s域模型
- 卷积
若
![[公式]](/images/download/1656037217431_20901.png) 为有始信号,则
为有始信号,则![[公式]](/images/download/1656037217607_73619.png)
- 初值
若
![[公式]](/images/download/1656037217831_31684.png) ,则
,则 ![[公式]](/images/download/1656037218055_82554.png)
若
![[公式]](/images/download/1656037218194_60357.png) 不为真分式,应化为真分式:
不为真分式,应化为真分式:![[公式]](/images/download/1656037218308_93843.png)
![[公式]](/images/download/1656037218435_92685.png)
- 终值(自控还会用到)
若
![[公式]](/images/download/1656037218863_76767.png) ,则
,则 ![[公式]](/images/download/1656037219077_76402.png)
终值存在的条件:
![[公式]](/images/download/1656037219216_77429.png) 在右半平面和
在右半平面和 ![[公式]](/images/download/1656037219329_36461.png) 轴(原点除外)上无极点
轴(原点除外)上无极点- 对s域微分
若
![[公式]](/images/download/1656037219441_14200.png) ,则
,则 ![[公式]](/images/download/1656037219596_81683.png)
- 对s域积分
若
![[公式]](/images/download/1656037219735_21950.png) ,则
,则 ![[公式]](/images/download/1656037219876_22614.png)
- 拉普拉斯逆变换
- 由象函数求原函数的三种方法
- 部分分式法
- 利用留数定理——围线积分法
- 数值计算方法——利用计算机
- 部分分式法求拉氏逆变换
- 第一种情况:单阶实数极点
- 找极点,展开,逆变换
- 求系数:左右同乘(s+k),再令s=-k
- 第二种情况:极点为共轭复数(除了以下方法,还可以化为sin、cos的s域形式)
共轭极点出现在
![[公式]](/images/download/1656037220037_97531.png) ,
, ![[公式]](/images/download/1656037220218_85299.png)
其中
![[公式]](/images/download/1656037220360_27358.png) 成共轭关系,
成共轭关系, ![[公式]](/images/download/1656037220522_39089.png)
则
![[公式]](/images/download/1656037220941_16866.png)
- 第三种情况:有重根存在——除了两边同乘(s+k)^n,还要两边求导
- 两种特殊情况
- 非真分式——化为真分式+多项式(长除法)
- 含有e^(-s)的非有理式——利用时移性质
- 用拉普拉斯变换法分析电路、s域元件模型
- 用拉氏变换法分析电路的步骤
- 列s域方程(先时域,或直接s域)
- 求解s域方程
- 逆变换
- 微分方程的拉氏变换
- 采用0-系统求解
- 先求起始状态
- 利用元件的s域模型分析电路
- 系统函数(网络函数)H(s)
- 系统函数
- 定义
- 分类
- 策动点函数:激励与响应在同一端口时
策动点导纳
![[公式]](/images/download/1656037221115_77747.png) ;策动点阻抗
;策动点阻抗 ![[公式]](/images/download/1656037221305_80613.png)
- 转移函数:激励和响应不在同一端口
转移导纳
![[公式]](/images/download/1656037221449_81333.png) ;转移阻抗
;转移阻抗 ![[公式]](/images/download/1656037221629_47767.png) ;电压比
;电压比 ![[公式]](/images/download/1656037221785_79747.png) ;电流比
;电流比 ![[公式]](/images/download/1656037221941_67184.png)
- 求H(s)的方法:定义,或由h(t)得到(单位冲激的零状态响应)
- 应用:求系统的零状态响应
![[公式]](/images/download/1656037222091_52480.png) 或
或 ![[公式]](/images/download/1656037222245_88889.png)
- LTI互联网络的系统函数
- LTI系统的并联:和
- LTI系统的级联:时域卷积,频域乘积
- LTI系统的反馈连接(同自控原理,H1/(H1H2+1))
- 由系统函数零、极点分布决定时域特性
- H(s)零、极点与h(t)波形特征的对应(自控会经常用到)
- H(s) 、E(s)的极点分布与自由响应、强迫响应特性的对应
- 系统函数的极点→自由响应分量;激励函数的极点→强迫响应分量
- 定义系统行列式(特征方程)的根为系统的固有频率(或称“自然频率”、“自由频率”);H(s)的极点都是系统的固有频率;H(s)零、极点相消时,某些固有频率将丢失
- 自由响应的极点只由系统本身的特性所决定,与激励函数的形式无关,然而系数与H(s)、E(s)都有关
- 左半平面极点产生的函数项对应暂态响应
- 零输入、零状态可由R(s)式中有无初始状态区分
- 由系统函数零、极点分布决定频响特性
- 定义
- “频响特性”:指系统在正弦信号激励下稳态响应随频率的变化情况
- 前提:稳定的因果系统(有实际意义的物理系统都是稳定的因果系统)
- H(s)和频响特性的关系——幅频特性,相频特性
![[公式]](/images/download/1656037222499_62760.png)
- 几种常见的滤波器
- 根据H(s)零极点图绘制系统的频响特性曲线
- 画零极点图
- 由矢量图确定频率响应特性
![[公式]](/images/download/1656037222698_64139.png)
- 全通函数与最小相移函数的零、极点分布
- 全通网络:幅频特性为常数,对于全部频率的正弦信号都能按同样的幅度传输系数通过
- 零、极点分布:极左零右,关于虚轴对称
- 幅频特性等于常数K
- 相频特性不受约束
- 在传输系统中常用来进行相位校正,例如,作相位均衡器或移相器
- 最小相移网络:只在左半平面或虚轴有零点
- 级联:非最小相移网络可代之以最小相移网络与全通网络的级联
- 线性系统的稳定性
- 定义(BIBO):一个系统,如果对任意的有界输入,其零状态响应也是有界的,则称该系统有界输入有界输出(BIBO)稳定的系统,简称稳定系统
- 由H(s)的极点位置判断系统稳定性
若H(s)的全部极点位于s平面的左半平面(不包括虚轴)则满足
![[公式]](/images/download/1656037223004_63495.png) ,系统是稳定的
,系统是稳定的- 拉普拉斯变换与傅里叶变换的关系
- 存在傅里叶变换的条件
当
![[公式]](/images/download/1656037223181_12816.png) 时,收敛边界落于s平面左半边,傅氏变换存在
时,收敛边界落于s平面左半边,傅氏变换存在 ![[公式]](/images/download/1656037223317_40093.png)
- 特殊:收敛边界在虚轴
F(s)是存在的,
![[公式]](/images/download/1656037223465_65384.png) 和
和 ![[公式]](/images/download/1656037223596_76012.png) 之间不再是简单的置换关系,因为傅氏变换中包括奇异函数项
之间不再是简单的置换关系,因为傅氏变换中包括奇异函数项- 收敛边界在虚轴,由F(s)求F(w)
- 只有一阶极点的情况,极点位于虚轴
![[公式]](/images/download/1656037223730_98295.png)
- 用卷积定理拆开,分别求
- 傅里叶变换应用于通信系统——滤波、调制与抽样
- 系统函数H(jω)及傅里叶变换分析法
- 傅里叶变换形式的系统函数
![[公式]](/images/download/1656037223892_15955.png)
- 频率响应特性
- 系统函数的物理意义
- 系统可以看作是一个信号处理器,对信号各频率分量进行加权。信号的幅度由
![[公式]](/images/download/1656037224035_25061.png) 加权信号的相位由
加权信号的相位由 ![[公式]](/images/download/1656037224180_39748.png) 修正
修正 - 对于不同的频率w,有不同的加权作用,这也是信号分解,求响应再叠加的过程
![[公式]](/images/download/1656037224313_72611.png)
- 利用系统函数H(jω)求响应
- 系统的频响特性与H(s)的关系
- 正弦信号激励下的稳态响应
设激励信号为
![[公式]](/images/download/1656037224484_13318.png) ,系统的频率响应为
,系统的频率响应为 ![[公式]](/images/download/1656037224620_99331.png) ,则系统的稳态响应为
,则系统的稳态响应为 ![[公式]](/images/download/1656037224795_10040.png)
- 无失真传输
- 失真
- 幅度失真;相位失真
- 线性系统的失真——幅度、相位变化,不产生新的频率成分
- 非线性系统产生非线性失真——产生新的频率成分
- 无失真传输条件
时域:
![[公式]](/images/download/1656037224950_37839.png)
频域:
![[公式]](/images/download/1656037225134_83008.png)
- 利用失真——波形形成
- 理想低通滤波器模型
- 理想低通的频率特性
- 理想低通的冲激响应
![[公式]](/images/download/1656037225319_72549.png)
- 比较输入输出,可见严重失真
- 理想低通滤波器是个物理不可实现的非因果系统
- 理想低通的阶跃响应
![[公式]](/images/download/1656037225590_81546.png) ,其中正弦积分
,其中正弦积分 ![[公式]](/images/download/1656037225758_95779.png)
- 上升时间:输出由最小值到最大值所经历的时间,即
![[公式]](/images/download/1656037226300_71225.png) ,B是将角频率折合为频率的滤波器带宽(截止频率)
,B是将角频率折合为频率的滤波器带宽(截止频率) - 阶跃响应的上升时间tr与网络的截止频率B(带宽)成反比
- 理想低通对矩形脉冲的响应
- 调制/解调的原理与实现
- 调制原理
- 调制:将信号的频谱搬移到任何所需的较高频段上的过程
- 幅度调制
- 解调:将已调信号恢复成原来的调制信号的过程
- 调幅、抑制载波调幅及其解调波形
- 频分复用
- 复用:在一个信道上传输多路信号
- 频分复用:就是以频段分割的方法在一个信道内实现多路通信的传输体制
- 复用——发信端
- 复用——收信端:带通滤波器
- 带通系统的运用
- 调幅信号作用于带通系统【实际运用】
- 如果调制信号具有多个频率分量,为保证传输波形的包络不失真,要求理想带通滤波器
- 用带通系统传输调幅波的过程中,只关心包络波形是否产生失真,并不注意载波相位如何变化
- 频率窗函数的运用:希望观察信号在时域或频域的局部性能时,可用“窗函数”对信号开窗【理论运用】
- 系统的状态变量分析
- 引言
- 输入-输出法(端口法)
- 状态变量分析法
- 名词定义:状态、状态变量、状态矢量、状态空间、状态轨迹
- 连续时间系统状态方程的建立
- 状态方程的一般形式和建立方法概述
状态方程:
![[公式]](/images/download/1656037226611_37814.png)
输出方程:
![[公式]](/images/download/1656037226779_68851.png)
- 由电路图直接建立状态方程
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=966

Best Last Month
Information industry by wittx
Information industry by wittx
Information industry by wittx
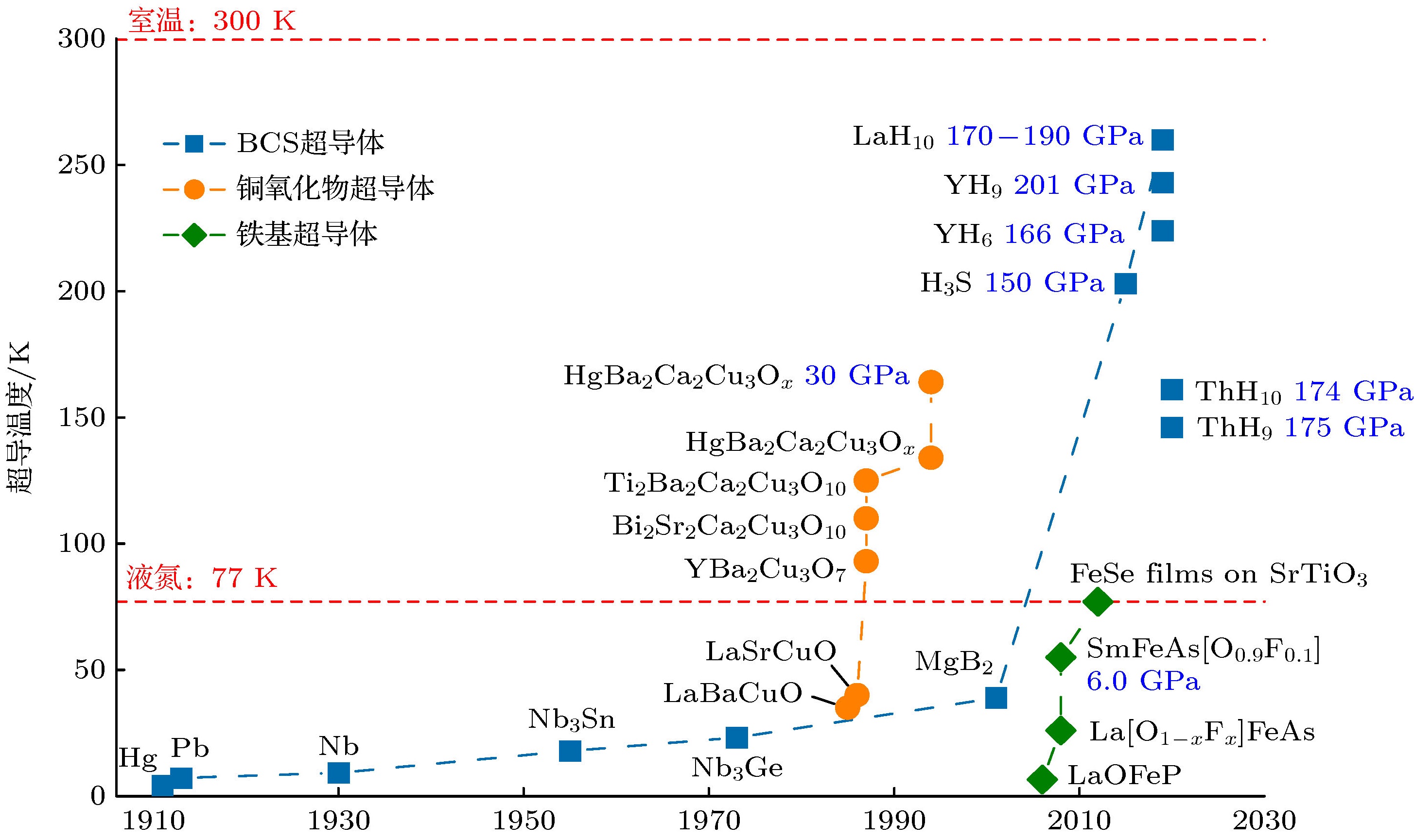
Information industry by wittxSuperconductor Pb10-xCux(PO4)6O showing levitation at room temperature and atmospheric pressure
.jpg)
Information industry by wittx
Information industry by wittx

Information industry by wittx
Information industry by wittx
Information industry by wittx
Information industry by wittxBatch Prompting: Efficient Inference with Large Language Model APIs

























