
- Investment
- 科学论坛
-
Program
- Recruitment
- Center
News Message
数字信号解析
- by wittx 2022-06-24
问题:
设计一个滤波器对录制一段语音(16kHz采样,16 bit 量化,长度约3秒)信号进行滤波。滤波器指标为:截止频率为[300Hz, 3400Hz],低频过渡带宽60Hz,高频过渡带宽为200Hz,通带纹波 小于0.1dB,阻带衰减大于60dB。设计一个满足该指标的FIR滤波器和IIR滤波器,给出其频率响应特性,并验证其是否符合上述指标要求,以及其是否满足线性相位?用这两个滤波器分别对该段语音进行滤波,分析比较滤波前后信号的波形和频谱。
欢迎关注,点赞,转发,共同学习【谢谢鼓励!!!】
语音信号滤波处理步骤如下:
- 录制语音信号
先利用MATLAB语音信号工具箱的audiorecorder函数录制一段时间长度约3秒,采样频率为16kHz,位数量化为16 bit的语音信号,并画出这段语音信号的时域和频域的波形如图1.1所示
图1.1 录音信号时域和频域的波形
2. FIR和IIR数字滤波器的选择
IIR滤波器和FIR滤波器的设计方法不同,IIR滤波器设计方法有间接法和直接法,间接法是借助于模拟滤波器的设计方法进行的。其设计步骤是:先设计过渡模拟滤波器得到系统函数H(s),然后将H(s)按某种方法转换成数字滤波器的系统函数H(z)。FIR滤波器必须采用间接法,常用的方法有窗函数法、频率采样法和切比雪夫等波纹逼近法。对于线性相位滤波器,经常采用FIR滤波器。
数字滤波器有很多种,根据其实现的网络结构或者其冲激响应函数的时域特性,可分为两种:有限冲激响应( FIR,Finite Impulse Response)滤波器和无限冲激响应( IIR,Infinite Impulse Response)滤波器。在设计FIR滤波器时可以根据对阻带衰减及过渡带的指标要求,选择串窗数类型(矩形窗、三角窗、汉宁窗、汉明窗、凯塞窗等),并估计窗口长度N,先按照阻带衰减选择窗函数类型。保证阻带衰减满足要求的情况下,尽量选择主瓣的窗函数,再构造希望逼近的频率响应函数,计算h(n)。最后加窗便可以得到设计结果。在设计IIR滤波器时可以借助成熟的模拟滤波器的成果,如巴特沃斯、契比雪夫和椭圆滤波器等,根据指标先写出模拟滤波器的公式,然后通过一定的变换,将模拟滤波器的公式转换成数字滤波器的公式。
由实验滤波器指标:截止频率为[300Hz, 3400Hz],低频过渡带宽60Hz,高频过渡带宽为200Hz,通带纹波小于0.1dB,阻带衰减大于60dB。可得
通带下限截止频率:fp1=300;
通带上线截止频率:fp2=3400;
阻带下线截止频率:fs1=240;
阻带上限截止频率:fs2=3600;
通带最大衰减:Rp=0.1;
阻带最小衰减:Rs=60;
由以上数据可知所叙述设计滤波器为带通滤波器,又因为阻带衰减大于60dB,通带纹波小于0.1dB,经查凯瑟窗满足阻带和通带的衰减条件,可选凯瑟窗设计FIR滤波器。在进行IIR滤波器设计过程中曾尝试通过巴特沃斯数字滤波器和切比雪夫数字滤波器,但都把语音信号的波形全部滤除为0结果如图2.1所示。总结原因是因为巴特沃斯数字滤波器和切比雪夫数字滤波通带衰减较大,不满足实验滤波器指标要求。而选用椭圆形滤波器设计带通滤波设计时对波形的处理相对较好,所以采用椭圆形滤波器进行IIR滤波器的设计。
图2.1 巴特沃斯滤波器对语音信号滤波结果
3. FIR和IIR数字滤波器的设计
以上已经论述设计FIR数字滤波器时采用凯瑟窗来实现,按要求的滤波器指标进行频率归一化计算,求过渡带宽和凯瑟窗长度并利用w=kaiser(L,beta)求凯瑟窗函数,具体方法如下:
wp1=2*pi*fp1/fs;wp2=2*pi*fp2/fs; %频率归一化计算
ws1=2*pi*fs1/fs;ws2=2*pi*fs2/fs;
deltaw=min((wp1-ws1),(ws2-wp2)); %计算通带滤波器过渡带w
N=ceil(7.24*pi/deltaw); %凯瑟窗长度
wd=(kaiser(N,5.658))'; %求凯瑟窗函数
b=fir1(n,Wn)是基于窗函数的有限脉冲响应滤波器设计,以此可以间接构造FIR滤波器。IIR滤波器的设计跟FIR有所不同,可以采用设计模拟滤波器的方法来间接实现,具体方法是将频率归一化计算后通过函数[n,Wp]=ellipord(Wp,Ws,Rp,Rs,'s')确定滤波器的阶数和截止频率,然后调用[a,b]=ellip (n,Rs, Wn,'s')确定系统函数的分子分母,再把模拟滤波器转换为数字滤波器便构造IIR滤波器。运行所设计的相应MATLAB程序可分别得到满足滤波器性能指标的凯瑟窗函数波形及其幅频响应和椭圆型滤波器的幅频响应,如图3.1和图3.2所示
图3.1 凯瑟窗函数波形及其幅频响应
图3.2 椭圆型滤波器的幅频响应
总结分析可知,通过FIR和IIR数字滤波器的频谱图形可知所设计的滤波器满足实验性能指标要求。FIR滤波器结构上主要是非递归结构,没有输出到输入的反馈,FIR数字滤波器的幅频特性精度较之于IIR数字滤波器低,但是不同频率分量的信号经过fir滤波器后他们的时间差不变,是线性相位。IIR滤波器采用递归型结构,即结构上带有反馈环路。IIR滤波器运算结构通常由延时、乘以系数和相加等基本运算组成,可以组合成直接型、正准型、级联型、并联型四种结构形式,都具有反馈回路。FIR数字滤波器是有限的单位响应也有利于对数字信号的处理,便于编程,用于计算的时延也小,这对实时的信号处理很重要。FIR滤波器因具有系统稳定,易实现相位控制,允许设计多通带(或多阻带)滤波器等优点。但FIR 阶数远高于IIR阶数,而阶数越大,设计越复杂,在实际中越难以实现。IIR可以用较低的阶数实现较高的带通选择性。
一、 用设计FIR和IIR数字滤波器处理录音信号
音频信号通过IIR数字滤波器需要调用filter函数,调用格式:y=filter(b,a,x),filter采用数字滤波器对数据进行滤波,既可用于IIR滤波器也可用于FIR滤波器。y=filter(b,a,x)利用给出的矢量a和b,对x中的数据进行滤波,结果放入y矢量。
将自行录制一段16kHz采样、16 bit 量化、长度约3秒的录音信号通过函数y= getaudiodata()量化为double类型数据返回给y,再分别用所设计FIR和IIR数字滤波器进行滤波。得到经过FIR滤波后时域波形如图4.1(a)所示、FIR滤波后信号的幅频响应如图4.1(b)所示、经过IIR滤波器滤波后时域波形如图4.2(a)所示、IIR滤波后的幅频响应如图4.2(b)所示。
图4.1(a) 经过FIR滤波后时域波形
图4.1(b) FIR滤波后信号的幅频响应
图4.2(a) 经过IIR滤波器滤波后时域波形
图4.2(b) IIR滤波后的幅频响应
结论总结:通过观察FIR滤波器处理后的语音信号与原始信号的时域和频域的波形可以发现录音信号的超过3600Hz的高频和低于240Hz的低频部分都被滤除掉,频谱波形变得更加清晰,但幅值有所衰减。通过观察IIR滤波器处理后时域和频谱图可知虽然也想FIR处理后的一样频谱更加清晰,但是幅度衰减并没有那么明显,比FIR滤波器的幅频性能好。
可在Matlab中用函数sound对声音进行回放。其调用格式:sound(y,Fs),sound(y)和sound(y,Fs,bits)。可以察觉滤波前后的声音有明显的变化。通过上面的频谱图可以很清晰地观察到经过滤波后与滤波前存在明显差别,滤波后的频谱更加频谱清晰,经过FIR和IIR滤波处理后的声音都显得比较平缓,有种机械的感觉,但IIR滤波后的声音更加柔和一些。因为原始信号经过带通通滤波器后,带通滤波器会把信号低频和高频部分滤掉,只剩下 [300Hz,3400Hz]中间部分的频率。
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=965

Best Last Month
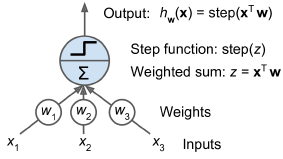
Mechanical electromechanical by wittx
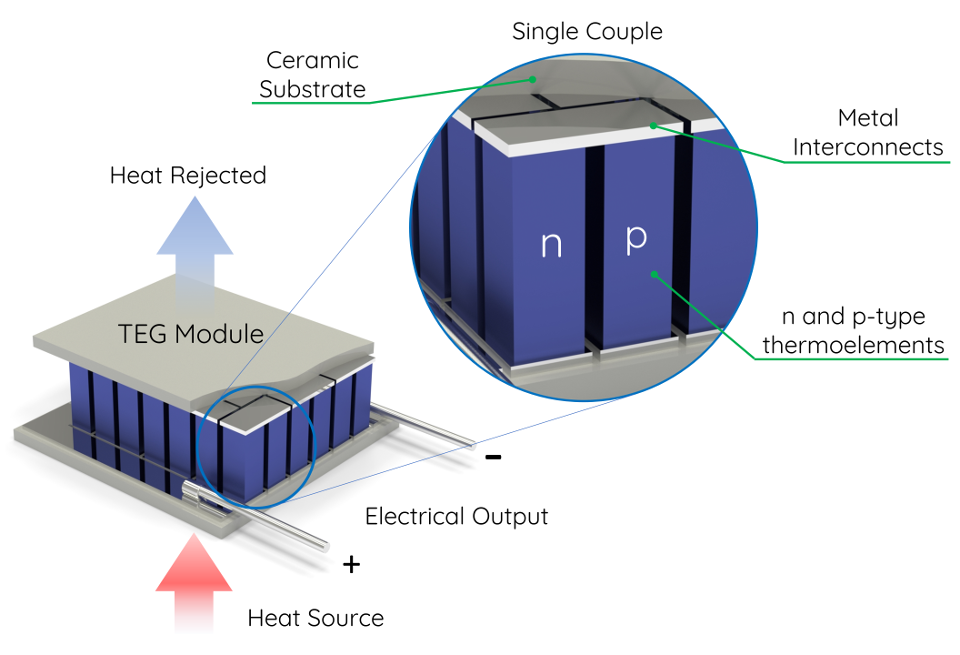
Information industry by wittxThree dimensional architected thermoelectric devices with high toughness and power conversion effici

Information industry by wittx

Information industry by wittx
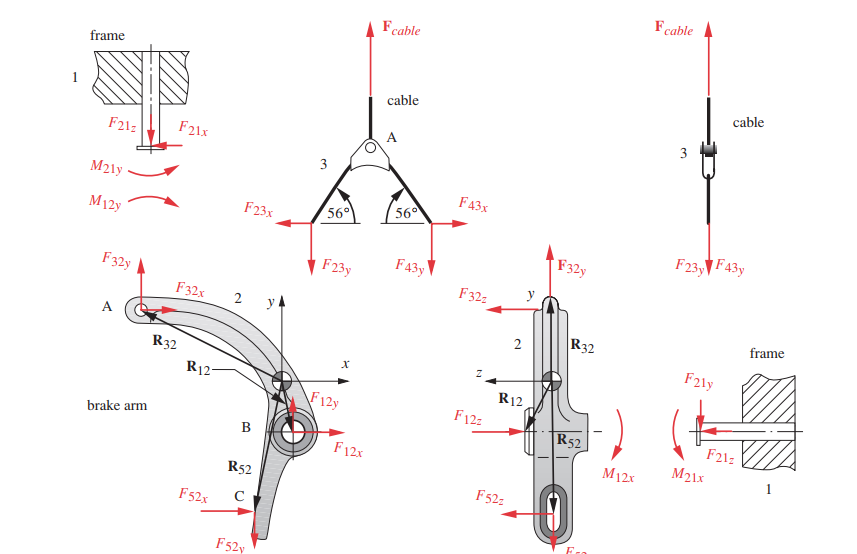
Information industry by wittx
.jpg)
Traffic by wittx

Information industry by wittx
Information industry by wittx
Information industry by wittx
Mechanical electromechanical by wittx









