
- Investment
- 科学论坛
-
Program
- Recruitment
- Center
News Message
网络规模更小、速度更快,MorphNet
- by wittx 2022-06-20
深度神经网络(DNN)在解决图像分类、文本识别和语音转录等实际难题方面显示出卓越的效能。但是,为给定问题设计合适的 DNN 架构依然是一项具有挑战性的任务。考虑到巨大的架构搜索空间,就计算资源和时间而言,为具体应用从零开始设计一个网络是极其昂贵的。神经架构搜索(NAS)和 AdaNet 等方法使用机器学习来搜索架构设计空间,从而找出适合的改进版架构。另一种方法是利用现有架构来解决类似问题,即针对手头任务一次性对架构进行优化。
谷歌研究人员提出一种神经网络模型改进的复杂方法 MorphNet。研究人员发表了论文《MorphNet: Fast & Simple Resource-Constrained Structure Learning of Deep Networks》,MorphNet 将现有神经网络作为输入,为新问题生成规模更小、速度更快、性能更好的新神经网络。研究人员已经运用该方法解决大规模问题,设计出规模更小、准确率更高的产品服务网络。目前,MorphNet 的 TensoreFlow 实现已开源,大家可以利用该方法更高效地创建自己的模型。
MorphNet 开源项目地址:https://github.com/google-research/morph-net
MorphNet 的工作原理
MorphNet 通过收缩和扩展阶段的循环来优化神经网络。在收缩阶段,MorphNet 通过稀疏性正则化项(sparsifying regularizer)识别出效率低的神经元,并将它们从网络中去除,因而该网络的总损失函数包含每一神经元的成本。但是对于所有神经元,MorphNet 没有采用统一的成本度量,而是计算神经元相对于目标资源的成本。随着训练的继续进行,优化器在计算梯度时是了解资源成本信息的,从而得知哪些神经元的资源效率高,哪些神经元可以去除。
MorphNet 的算法 例如,考虑一下 MorphNet 如何计算神经网络的计算成本(如 FLOPs)。为简单起见,我们来思考一下被表示为矩阵乘法的神经网络层。在这种情况下,神经网络层拥有 2 个输入(x_n)、6 个权重 (a,b,...,f) 和 3 个输出(y_n)。使用标准教科书中行和列相乘的方法,你会发现评估该神经网络层需要 6 次乘法。
神经元的计算成本 MorphNet 将其计算成本表示为输入数和输出数的乘积。请注意,尽管左边示例显示出了权重稀疏性,其中两个权重值为 0,但我们依然需要执行所有的乘法,以评估该神经网络层。但是,中间示例显示出了结构性的稀疏,其中神经元 y_n 最后一行上的所有权重值均为 0。MorphNet 意识到该层的新输出数为 2,并且该层的乘次数量由 6 降至 4。基于此,MorphNet 可以确定该神经网络中每一神经元的增量成本,从而生成更高效的模型(右边示例),其中神经元 y_3 被移除。
在扩展阶段,研究人员使用宽度乘数(width multiplier)来统一扩展所有层的大小。例如,如果层大小扩大 50%,则一个效率低的层(开始有 100 个神经元,之后缩小至 10 个神经元)将能够扩展回 15,而只缩小至 80 个神经元的重要层可能扩展至 120,并且拥有更多资源。净效应则是将计算资源从该网络效率低的部分重新分配给更有用的部分。
用户可以在收缩阶段之后停止 MorphNet,从而削减该网络规模,使之符合更紧凑的资源预算。这可以在目标成本方面获得更高效的网络,但有时可能导致准确率下降。或者,用户也可以完成扩展阶段,这将与最初目标资源相匹配,但准确率会更高。
为什么使用 MorphNet?
MorphNet 可提供以下四个关键价值:
有针对性的正则化:MorphNet 采用的正则化方法比其他稀疏性正则化方法更有目的性。具体来说,MorphNet 方法用于更好的稀疏化,但它的目标是减少资源(如每次推断的 FLOPs 或模型大小)。这可以更好地控制由 MorphNet 推导出的网络结构,这些网络结构根据应用领域和约束而出现显著差异。
例如,下图左展示了在 JFT 数据集上训练的 ResNet-101 基线网络。在指定目标 FLOPs(FLOPs 降低 40%,中间图)或模型大小(权重减少 43%,右图)的情况下,MorphNet 输出的结构具有很大差异。在优化计算成本时,相比于网络较高层中的低分辨率神经元,较低层中的高分辨率神经元会被更多地修剪掉。当目标是较小的模型大小时,剪枝策略相反。
MorphNet 有目标性的正则化(Targeted Regularization)。矩形的宽度与层级中通道数成正比,底部的紫色条表示输入层。左:输入到 MorphNet 的基线网络;中:应用 FLOP regularizer 后的输出结果;右:应用 size regularizer 后的输出结果。
MorphNet 能够把特定的优化参数作为目标,这使得它可针对特定实现设立具体参数目标。例如,你可以把「延迟」作为整合设备特定计算时间和记忆时间的首要优化参数。
拓扑变换(Topology Morphing):MorphNet 学习每一层的神经元,因此该算法可能会遇到将一层中所有神经元全都稀疏化的特殊情况。当一层中的神经元数量为 0 时,它切断了受影响的网络分支,从而有效地改变了网络的拓扑结构。例如,在 ResNet 架构中,MorphNet 可能保留残差连接,但移除残差模块(如下图左所示)。对于 Inception 结构,MorphNet 可能移除整个并行分支(如下图右所示)。
左:MorphNet 移除 ResNet 网络中的残差模块。右:MorphNet 移除 Inception 网络中的并行分支。 可扩展性:MorphNet 在单次训练运行中学习新的网络结构,当你的训练预算有限时,这是一种很棒的方法。MorphNet 还可直接用于昂贵的网络和数据集。例如,在上述对比中,MorphNet 直接用于 ResNet-101,后者是在 JFT 数据集上以极高计算成本训练出的。
可移植性:MorphNet 输出的网络具备可移植性,因为它们可以从头开始训练,且模型权重并未与架构学习过程绑定。你不必复制检查点或按照特定的训练脚本执行训练,只需正常训练新网络即可。
Morphing Network
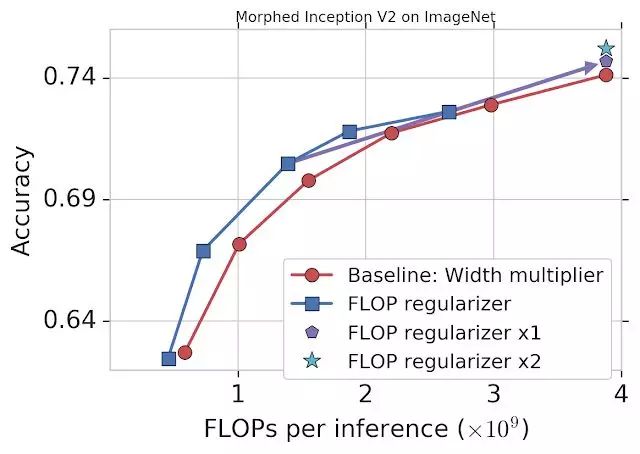
谷歌通过固定 FLOPs 将 MorphNet 应用到在 ImageNet 数据集上训练的 Inception V2 模型上(详见下图)。基线方法统一缩小每个卷积的输出,使用 width multiplier 权衡准确率和 FLOPs(红色)。而 MorphNet 方法在缩小模型时直接固定 FLOPs,生成更好的权衡曲线。在相同准确率的情况下,新方法的 FLOP 成本比基线低 11%-15%。
将 MorphNet 应用于在 ImageNet 数据集上训练的 Inception V2 模型后的表现。仅使用 flop regularizer(蓝色)的性能比基线(红色)性能高出 11-15%。一个完整循环之后(包括 flop regularizer 和 width multiplier),在相同成本的情况下模型的准确率有所提升(「x1」,紫色),第二个循环之后,模型性能得到继续提升(「x2」,青色)。
这时,你可以选择一个 MorphNet 网络来满足更小的 FLOP 预算。或者,你可以将网络扩展回原始 FLOP 成本来完成缩放周期,从而以相同的成本得到更好的准确率(紫色)。再次重复 MorphNet 缩小/放大将再次提升准确率(青色),使整体准确率提升 1.1%。
结论
谷歌已经将 MorphNet 应用到其多个生产级图像处理模型中。MorphNet 可带来模型大小/FLOPs 的显著降低,且几乎不会造成质量损失。
论文:MorphNet: Fast & Simple Resource-Constrained Structure Learning of Deep
论文链接:https://arxiv.org/pdf/1711.06798.pdf
摘要:本研究介绍了一种自动化神经网络结构设计的新方法 MorphNet。MorphNet 迭代地放缩网络,具体来说,它通过激活函数上的资源权重(resource-weighted)稀疏性正则化项来缩小网络,通过在所有层上执行统一的乘积因子(multiplicative factor)来放大网络。MorphNet 可扩展至大型网络,对特定的资源约束具备适应性(如 FLOPs per inference),且能够提升网络性能。把 MorphNet 应用到大量数据集上训练的标准网络架构时,该方法可以在每个领域中发现新的结构,且在有限资源条件下提升网络的性能。
原文链接:https://ai.googleblog.com/2019/04/morphnet-towards-faster-and-smaller.html
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=954

Best Last Month
Information industry by wittx

Information industry by wittx

Information industry by wittx
Information industry by wittx
Computer software and hardware by wittx
Information industry by wittx
Information industry by wittx
Information industry by wittx

Information industry by wittx
Information industry by wittx







