-
News Message
魔角石墨烯的荷电斯格明子和超导性的拓扑学起源
- by wittx 2022-06-20
通常情况下，当向绝缘体中添加电荷时，会产生电子或空穴激发，从而导致电荷传导。然而，孤子能起到载流子的作用吗？在理论上，这种不寻常的场景可以通过带电的拓扑结构来实现。实验上唯一确定的例子发生在量子霍尔铁磁体中。唯一通过实验建立的实例发生在量子霍尔铁磁体中，其中斯格明子形式的自旋拓扑结构由于Landau能级拓扑结构而获得电荷，并且被发现是能量最低的电荷激发。另一方面，找到带电拓扑结构之间而不是电子之间发生Cooper配对的情况更加艰难。例如，在前面已经通过实验建立带电拓扑结构的量子霍尔铁磁体中，时间反转对称性的强烈破坏使得超导性极不可能。从拓扑织构中获得强大的超导性通常需要同时满足两个条件：（i）不间断的时间反转对称性和（ii）稳定的低能量电荷2e拓扑结构存在。如果基本缺陷具有电荷2e或通过配对相同电荷的e缺陷，后者可以实现。
【成果简介】
近日，哈佛大学物理学院Ashvin Vishwanath教授团队证明了所有这些标准都满足于一个简单的模型，该模型由两个时间反转相关的量子霍尔（或平坦的Chern带）铁磁体组成，通过隧道耦合，具有纯粹的排斥相互作用。作者认为，这样一个模型捕捉到了魔角石墨烯的基本物理特性，使其成为由拓扑结构配对产生的超导性的有希望的候选者，这一机制与传统的电子-声子机制有本质的区别。该论文以题为“Charged skyrmions and topological origin of superconductivity in magic-angle graphene”发表在知名期刊Sci. Adv.上。
【图文导读】
图一、赝自旋的定义
扭曲双层石墨烯（左）的几乎平坦带的线性组合产生具有相反Chern数的赝自旋带。位于相反陈扇区的具有相同赝自旋的两个状态具有相同的谷波函数，但通过A-B亚晶格极化进行区分。
图二、隧道诱导超交换J
（上）Chern和赝自旋基对称性的作用。（中）从通过时间反演对称性相关的两个赝自旋铁磁体开始，色散h作为C2z𝒯相关状态（下）之间的隧道，导致超交换项J∼h2/U，作为赝自旋之间的反铁磁耦合与Chern扇区相反。
图三、Sigma模型参数
在介电常数ε = 9.5的情况和不同的栅极屏蔽距离d值下，赝自旋刚度（上）、反铁磁耦合J和赝自旋易面各向异性λ（下）与扭曲角θ的关系。
图四、带电拓扑结构的配对
（A）Chern扇区之一的单电荷e斯格明子。n+和n-中的赝自旋在斯格明子核心中没有反铁磁排列。
（B）n+-n-中的斯格明子-反斯格明子对由于反铁磁耦合J而结合在一起，这有利于局部赝自旋反排列形成一个电荷2e。
图五、带电激发的能量学
2e斯格明子的弹性能量与近手性（橙色）和实际（紫色）极限中的粒子-空穴带隙的比率，从自洽Hartree-Fock中提取刚度和带隙值。在灰色虚线下方，斯格明子能量位于粒子-空穴间隙内。
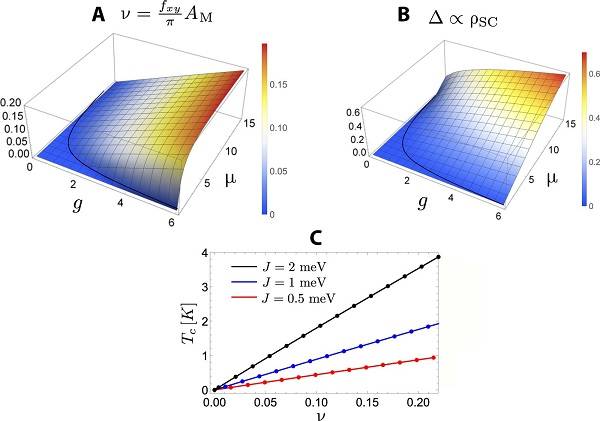
图六、掺杂CP1模型的大N相图
（A）荷电2e斯格明子填充分数ν的图，它与规整场aμ的通量fxy直接相关。
（B）自旋场∆的间隙，与超导相中的超流体刚度成正比。
（C）估算不同J值下CPN−1模型中的超导Tc。
图七、半填充v =2的魔角石墨烯
半填充时的自旋极化绝缘态有两种可能的情况：（A）相反的自旋带位于赝自旋反铁磁体的间隙内或（B）相反的自旋带位于该间隙外。
【结论展望】
魔角石墨烯中超导电性的发现及其出人意料之外，如果解释只援引常规成分，那将是出乎意料的。相反，作者认为这种观察需要一种不寻常的机制，如本文描述的斯格明子配对机制，它依赖于魔角石墨烯独特的性质。更普遍地说，作者已经从斥力中发现了超导电性的一种新机制，并且在未来探索各种其他环境将是有趣的，这些环境将实现与时间反转共轭体隧道耦合的Chern铁磁体的基本成分。
文献链接：Charged skyrmions and topological origin of superconductivity in magic-angle graphene (Sci. Adv. 2021, DOI: 10.1126/sciadv.abf5299)
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=952
Best Last Month
Information industry by wittx
Information industry by wittx
Information industry by wittx
![[Evolutionary Algorithm] 进化算法简](/witty_y/images/1613375829593_.jpg)
Information industry by show
Information industry by wittx
.jpeg)
Information industry by wittx
Information industry by wittx
Information industry by wittx
Information industry by wittx
Information industry by wittx
