
- Investment
- 科学论坛
-
Program
- Recruitment
- Center
News Message
转化效率、热电优值与功率因子
- by wittx 2022-03-19
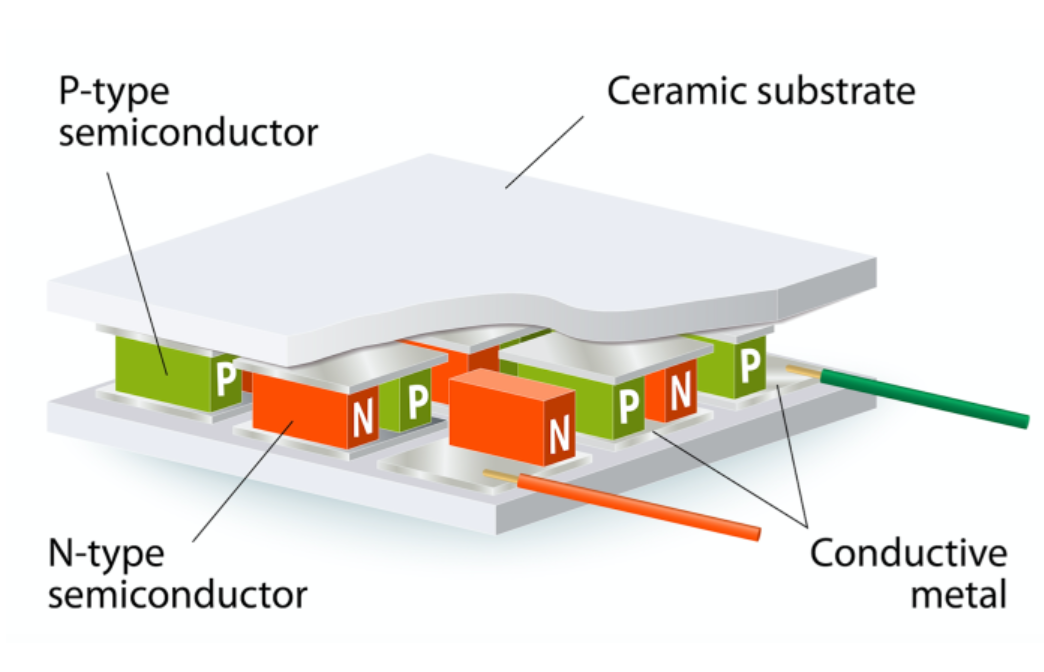
一、介绍
本期推文终于要将魔爪伸向在题图出现过这么多次的zT了~热电优值可以说是每个热电领域的研究人员必然十分熟悉的参数,绝大部分研究材料热电性能的文章最后都会放上zT,它的好处在于给所有不同体系的材料一个统一的标准来衡量其热电性能的好坏。那么它究竟是怎么定义出来的?为什么可以用它来作为标准?所谓的功率因子(Power Factor, PF)为什么如此命名?在热电基础(一)中我放过几本推荐阅读的书本,其中都有相关推导,但里面的步骤描述等可能不够详细,因此这里我以温差发电器件为例,详细讲一下是如何从转化效率过渡到热电优值的,希望能帮助大家更好地理解这些概念。
首先我们看一下zT的定义式进行直观上的理解:
其中Seebeck系数,电导率和热导率是材料的属性,我们知道温差发电器件基本原理便是Seebeck效应,在两端有温差时通过热电势发电。那么此时热电材料作为电源来看,在相同温差下S越大意味着电动势越大,而电导率越大意味着电源内阻越小,热导率则可以分两部分来看:1.热源给的热量一部分会转化为电能一部分会往冷端输运,热导率越大意味着更多的热量“浪费”了;2.要使用Seebeck效应需要材料两端建立起温差,而如果材料热导率越大,建立温差越困难。
综上所述,一个好的热电材料需要具有大的Seebeck系数,高电导率以及低热导率,和zT定义式中所包含的信息趋势一致,zT越大,意味着材料的热电性能越好。
接下来,在第二部分中,我们先补充一下Peltier效应的概念及参数关系,在第三、四部分中,我们会进行具体的公式推导,将器件最大转化效率与热电优值联系起来。在第五部分中,简单讲讲最大输出功率与功率因子的关系。
二、Peltier效应简介
Peltier效应可以说是Seebeck效应的逆效应,Seebeck效应讲的是在温差驱动下两种不同导体的闭合回路会产生额外的电势差(具体图像请回顾热电基础(一)),而Peltier效应则讲的是在电流驱动下两种不同导体的相接处会发生吸放热现象。
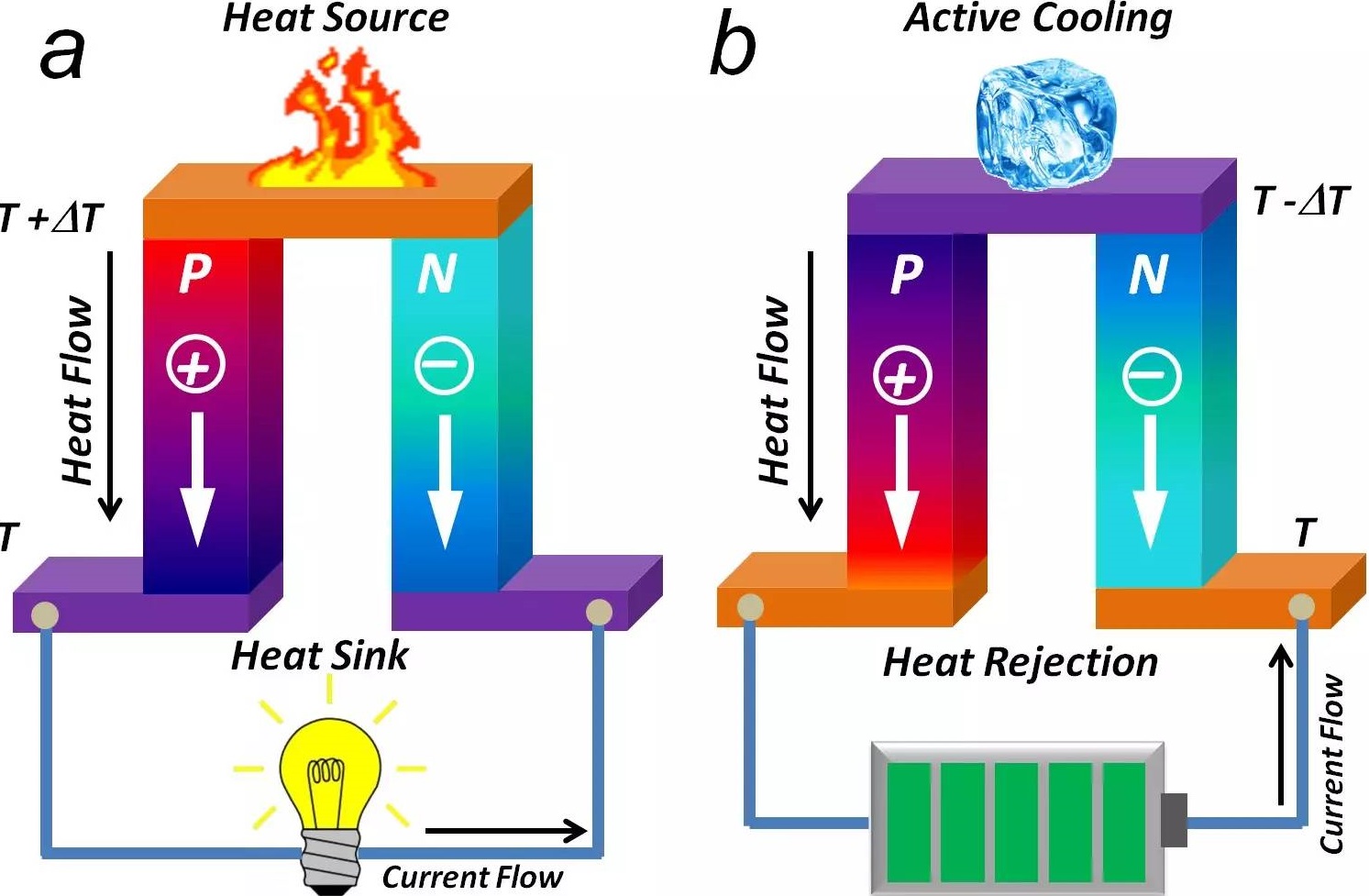
1834年法国科学家Peltier首次发现这个现象,他将金属Bi和Sb构成闭合回路,通入电流后发现在两个金属的接头处发生了水滴结冰的现象,电流反向后冰又融化成水。此效应的示意图和热电制冷器的一对热电臂如下图所示:
在材料两端温差不大时,吸放热速率和电流大小成正比,因此我们定义这两者的比值为Peltier系数,有如下关系:
其中q是吸放热速率,单位和功率相同(W),和Seebeck效应类似的,Peltier效应需要两种不同的材料才会出现,因此此处的πAB是AB两种材料的组合Peltier系数,可以类比之前说过的相对Seebeck系数和绝对Seebeck系数,左右两图的一致性我们此处就不再赘述了。
Peltier的物理图像也十分清晰,在电压驱动下载流子在材料中运动时不仅携带电荷,产生电流,也携带熵,产生熵流(热流),两种不同材料串联时,电流相同,但熵流往往不同,因此在相接处会对应的产生吸放热现象。我们看上方右图组成的一对热电臂的情况,对n型材料,电子携带着热量向下运动,而在p型材料中空穴携带着热量同样是向下运动,因此在这个图里上方会变成吸热端,下方则会放热。
而后,Thompson根据热力学关系导出了材料的Seebeck系数和Peltier系数存在如下关系:
具体的推导这里就不讲了,大家可以自行翻阅原文(平衡势力学近似:1857_PRSE:10.1017/S0370164600027310, 非可逆热力学1952书籍简介:10.1021/ed029p51.3)。在后面的公式推导中我们直接将这个关系作为结论使用。
三、温差发电器件的效率
(以下内容将开始公式推导和化简,希望大家不要被长公式吓到,并不会有超出高中数学的内容出现)
现在我们看一下一个温差发电器中存在的能量转化与热量流动情况,如下图所示:
此处我们需要作四个假设:
- 不考虑热电材料之外的诸如与电极陶瓷片之间连接所存在的电阻、热阻等造成的额外能量损失
- 系统处于稳态,冷热端温度固定不变化(分别为TH和TC)。
- 外界从热端输入能量保持热端温度,输入的能量全被器件热端吸收。
根据示意图和假设,不难看出热电流与Peltier热方向一致,均是从热端向冷端移动,傅里叶热也是如此。焦耳热在材料中均匀产生, 一半一半分别向冷热端传输。
在热端建立热平衡方程,接受到的热量为外界输入的热量QH以及传来的一半焦耳热0.5I²R,向下传输的热量为Peltier热πI以及傅里叶热K△T,其中R是热电臂总电阻,I是Seebeck电压在回路中产生的电流,K是热电臂总热导,意义是单位温差下通过的热流,具体方程表达式如下:
而回路电压就是Seebeck电压,假设外界负载电阻为RL,电流和输出功率容易表示为:
热电发电器件的效率定义为输出功率与外界输入热量之比,将电流公式代入热平衡方程,Peltier系数使用Kelvin关系替换为Seebeck系数(π=S*TH),上述公式即可转化为:
如此,当冷热端温度确定,材料的尺寸定完之后(热导、电阻确定)便得到了转化效率与外界负载电阻阻值之间的关系。
四、最大效率与热电优值
从上面的式子中,我们发现发电器件的外电阻与效率之间存在函数关系,将分子分母同除以负载阻值,RL的同类项进行合并,会发现分子是一个定值,分母则成为了一个对勾函数:
分母取到最小值时效率即可取得最大值,高中知识~根据基本不等式,有A/x+Bx≥2(根号AB),取等条件是前面两者相等,因此,效率有最大值时,负载电阻的阻值及其和内阻的关系为:
T上面一横是平均温度((TH+TC)/2),至此,我们可以定义出器件的热电优值Z为S²/RK,将此式带回效率的公式,可以得到最大效率:
至此,我们得到了器件最大转化效率与器件热电优值Z的关系,左边是卡诺循环效率,右边是与Z成正相关的一项,Z越大,越接近1,因此我们知道热电器件的效率的上限在卡诺循环效率之下。所以高温热电材料有一个天然的优势,它两端的温差可以拉的很大,虽然热电优值不一定很高,但是它的卡诺循环效率与室温材料相比可以大很多。
这里我们使用了一对热电臂的总电阻和总热导来定义器件的热电优值Z,具有温度的-1次方的量纲。而在热电基础(三)中我们提到,热流电流方向一致时,材料的电导与热导之比(或者热阻与电阻之比)便等于电导率和热导率之比,同时,考虑到Seebeck系数,电导率,热导率是有温度依赖关系的,因此习惯上我们用小写的z乘上T作为无量纲热电优值来描述材料在某个温度下的热电性能,对比如下:
不难理解材料的热电优值最终一定是和做成器件之后的优值成正相关的,至于如何从材料各性能的温度依赖关系推导出器件在理想条件下的转化效率,大家可以参考Jeff组的论文。(2017_EES: 10.1039/c7ee02007d)
五、最大输出功率与功率因子
这里我就不讲太多了,原理很简单,又是高中知识:当电源电动势和内阻确定的时候,负载电阻与内阻相同时有最大输出功率,即:
这里我直接把材料的功率因子也给出来了,容易知道当材料尺寸确定好之后最大输出功率便和功率因子直接成正比,这就是为什么我们会定义这样一个参数来描述它的电性能。
此时发电器件的热电转化效率是
可以看到仍然是和器件优值Z成正相关。
最大输出功率的意义在于有时候我们并不关心最终转化效率的高低,热源/废热就在那里,你能用它做出多少有用功就用多少,这时候减少它的利用量然后提升它的利用率反倒本末倒置了。但功率因子中只有电性能并不意味着此时我们不用关心材料的热导率了,第一部分我们提到过,热导率过高会导致难以在材料两端建立温差,所以虽然功率因子相同,高热导材料会导致△T过小从而电动势很小,同样输出不了多少功,因此在这种情况下zT仍然是一个较好的衡量标准。
简单总结一下,本期推文中我们介绍了Peltier效应,并以温差发电器件为例进行了效率的推导,得到了最大效率与器件热电优值之间的联系,也知道了最大输出功率与材料功率因子的对应关系。
再补充一句,器件的最大效率由卡诺循环效率和热电优值相关的两部分组成,因此,为了提高器件性能,除了增大材料本身的热电优值之外,高温热电材料在卡诺循环效率一项中占据优势,增大冷热端的工作温差也是提高器件效率的重要一环。
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=927

Best Last Month

Information industry by wittx
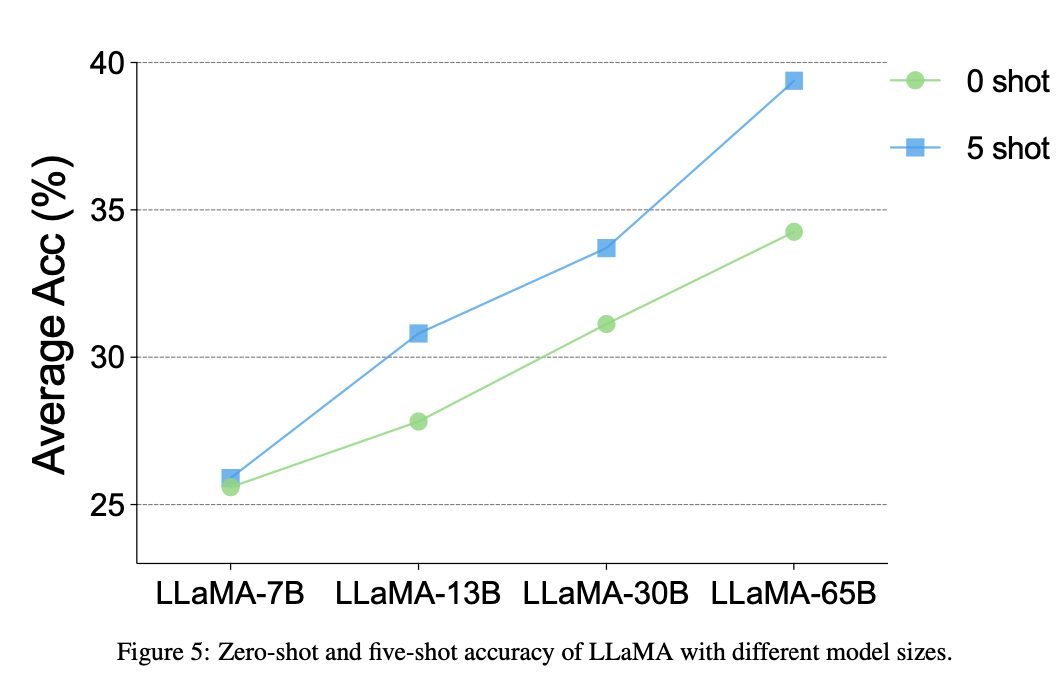
Information industry by wittxLLMs模型(GPTs、LaMDA、GLM/ChatGLM、PaLM/Flan-PaLM、BLOOM、LLaMA、Alpaca)
Information industry by wittx
Water conservancy and hydropower by wittx
Information industry by wittx
Information industry by wittxDeepFM: A Factorization-Machine based Neural Network for CTR Prediction
Material specialty by wittx
Information industry by wittx
Information industry by wittxNature High-efficiency solar thermoelectric conversion enabled by movable charging of molten salts

Information industry by wittx














