
- Investment
- 科学论坛
-
Program
News Message
电磁场的守恒定律:动量、能量与角动量
- by wittx 2022-03-19
能量守恒:坡印廷定理
假设区域
![[公式]](/images/download/1647674685662_95936.png) 中有电荷分布
中有电荷分布 ![[公式]](/images/download/1647674685842_12511.png) ,则单位体积上受到的电磁力为:
,则单位体积上受到的电磁力为:![[公式]](/images/download/1647674685987_57433.png)
电磁场做功为:
![[公式]](/images/download/1647674686158_17835.png)
注意到
![[公式]](/images/download/1647674686327_97808.png) ,故
,故 ![[公式]](/images/download/1647674686481_92184.png) 中第二项(也就是洛伦兹力项)不做功。所以全区域
中第二项(也就是洛伦兹力项)不做功。所以全区域 ![[公式]](/images/download/1647674686647_11425.png) 上电磁力总功率为:
上电磁力总功率为:![[公式]](/images/download/1647674686804_35201.png)
利用麦克斯韦方程组,把
![[公式]](/images/download/1647674687209_70873.png) 用场量表示:
用场量表示: ![[公式]](/images/download/1647674687359_52091.png)
![[公式]](/images/download/1647674687541_61019.png)
利用矢量微分法则:
![[公式]](/images/download/1647674687803_27426.png) 以及麦克斯韦方程组
以及麦克斯韦方程组 ![[公式]](/images/download/1647674687996_56419.png) 进一步化简:
进一步化简:![[公式]](/images/download/1647674688174_67576.png)
上式中,
![[公式]](/images/download/1647674688629_11582.png) 为坡印廷矢量,是电磁场单位时间内通过单位表面积向外部传递的能量。上式即为坡印廷定理。
为坡印廷矢量,是电磁场单位时间内通过单位表面积向外部传递的能量。上式即为坡印廷定理。上面定理等号左边为电磁场做功,它实际转化为了区域中粒子的机械能或其他形式能。右边第一项曲面积分即为此区域向外传递的能量,第二项即为区域中场能的变化。
若记区域中机械能的能量密度为
![[公式]](/images/download/1647674688812_98567.png) ,同时记
,同时记 ![[公式]](/images/download/1647674688965_55228.png) 为电磁场的能量密度,那么上式也可以写成微分形式:
为电磁场的能量密度,那么上式也可以写成微分形式:![[公式]](/images/download/1647674689217_12529.png)
以上是针对真空中的电磁场的讨论(或者说,我们不区分电荷/电流到底是自由电荷/电流还是束缚电荷/电流)。在介质中,我们更关心构建系统中自由电荷所需要的能量。这时需要把以上讨论中的电荷分布
![[公式]](/images/download/1647674689420_26339.png) 与电流分布
与电流分布 ![[公式]](/images/download/1647674689580_94179.png) 改为自由电荷分布
改为自由电荷分布 ![[公式]](/images/download/1647674689738_73882.png) 与自由电流分布
与自由电流分布 ![[公式]](/images/download/1647674689910_53658.png) ,推导中用到的麦克斯韦方程组改为介质中的。
,推导中用到的麦克斯韦方程组改为介质中的。![[公式]](/images/download/1647674690075_83118.png)
可见,此时电磁场能量密度的时间变化率为
![[公式]](/images/download/1647674690498_55981.png) (这里没有利用本构关系,请与线性介质下的公式相区分!)。坡印廷矢量变为
(这里没有利用本构关系,请与线性介质下的公式相区分!)。坡印廷矢量变为 ![[公式]](/images/download/1647674690671_38384.png) (同样地,这里也不需要知道本构关系)。
(同样地,这里也不需要知道本构关系)。动量守恒
现在考虑电磁场中粒子的动量。单位体积单位时间内粒子动量的变化即为单位体积上的电磁力
![[公式]](/images/download/1647674690819_74040.png) 。故对全空间:
。故对全空间:![[公式]](/images/download/1647674690961_36325.png)
利用麦克斯韦方程组,全部换成用场量表示:
![[公式]](/images/download/1647674691228_88157.png)
最后一步用到了分部积分,把对电场的时间偏导转成了对磁场的。利用麦克斯韦方程组进一步化简:
![[公式]](/images/download/1647674691552_70167.png)
在右式上再加一个恒为0的项
![[公式]](/images/download/1647674691843_73226.png) ,不会影响结果。利用矢量微分规则,继续化简:
,不会影响结果。利用矢量微分规则,继续化简:![[公式]](/images/download/1647674691993_17607.png)
我们定义麦克斯韦应力张量
![[公式]](/images/download/1647674692376_45372.png) :
: ![[公式]](/images/download/1647674692518_94234.png) ,其中
,其中 ![[公式]](/images/download/1647674692754_85277.png) 是Kronecker
是Kronecker ![[公式]](/images/download/1647674692960_65355.png) 符号。它的物理意义就是电磁场作用在单位表面积上的应力(压力/剪切应力)。然后就可以注 意 到
符号。它的物理意义就是电磁场作用在单位表面积上的应力(压力/剪切应力)。然后就可以注 意 到![[公式]](/images/download/1647674693106_49953.png)
(如果想要验证上式,只需把
![[公式]](/images/download/1647674693345_40397.png) 算符视为一个普通的向量,验证左右两边的各分量对应相等即可。)
算符视为一个普通的向量,验证左右两边的各分量对应相等即可。)这样,将动量式化简为
![[公式]](/images/download/1647674693492_99283.png)
这个式子结构上和坡印廷定理非常相似。等号左边是区域中粒子所受电磁力合力,也是(机械)动量变化率。等号右边第二项表示的是电磁场本身动量
![[公式]](/images/download/1647674693761_81467.png) 的时间变化率,第一项表示的是穿过区域边界流入的动量。
的时间变化率,第一项表示的是穿过区域边界流入的动量。若记区域中机械动量密度为
![[公式]](/images/download/1647674693929_37149.png) ,电磁场动量密度为
,电磁场动量密度为 ![[公式]](/images/download/1647674694097_86331.png) ,那么上式也可以写成微分形式:
,那么上式也可以写成微分形式:![[公式]](/images/download/1647674694270_39169.png)
这样,可以看出,
![[公式]](/images/download/1647674694447_83570.png) 表示动量流密度,
表示动量流密度, ![[公式]](/images/download/1647674694631_32916.png) 表示单位时间内通过
表示单位时间内通过 ![[公式]](/images/download/1647674694805_55558.png) 方向的单位面元沿
方向的单位面元沿 ![[公式]](/images/download/1647674694947_30860.png) 方向的动量。这是
方向的动量。这是 ![[公式]](/images/download/1647674695091_32306.png) 的另一个物理含义。
的另一个物理含义。以上是对真空中的电磁场的讨论。对于介质中的情况则非常复杂。事实上,除了在线性介质中,我们很难明确区分动量的来源从而给出场的动量的明确定义。在一般情况下,出于对这一问题的不同认识,可以得到不同形式的动量密度与麦克斯韦应力张量。因此,我就简单地类比之前的操作,用自由电荷分布
![[公式]](/images/download/1647674695280_88221.png) 与自由电流分布
与自由电流分布 ![[公式]](/images/download/1647674695432_24340.png) 来代替
来代替 ![[公式]](/images/download/1647674695609_65265.png) 和
和 ![[公式]](/images/download/1647674695777_66225.png) ,得到动量密度的一种形式:
,得到动量密度的一种形式:![[公式]](/images/download/1647674695948_77538.png)
我就暂时把最后一个式子的第一项写成张量的散度的形式了,只是定性地认为这一项表示了区域表面的动量流。而第二项则给出了介质中电磁场动量密度的闵可夫斯基形式:
![[公式]](/images/download/1647674696416_58957.png)
角动量守恒
由上面的推导知道,真空中电磁场的动量密度为
![[公式]](/images/download/1647674696637_74964.png) 。那么立刻可以知道真空中角动量密度为
。那么立刻可以知道真空中角动量密度为 ![[公式]](/images/download/1647674696828_11312.png) 。
。可见,只要
![[公式]](/images/download/1647674697009_56884.png) ,静场也会有动量和角动量。考虑经典的动量或角动量守恒时,必须要将电磁场的那一部分也包含在内,才能得到正确的结果。例如Feynman盘佯谬,在计算了电磁场的角动量以后仍然是守恒的。
,静场也会有动量和角动量。考虑经典的动量或角动量守恒时,必须要将电磁场的那一部分也包含在内,才能得到正确的结果。例如Feynman盘佯谬,在计算了电磁场的角动量以后仍然是守恒的。
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=926

Best Last Month
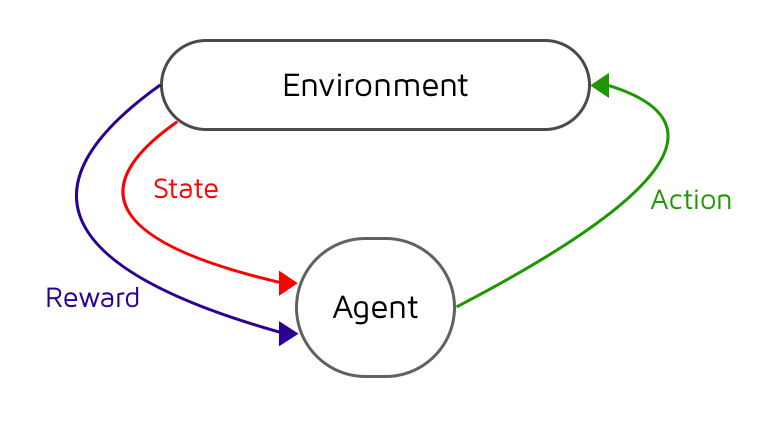
Information industry by AIMastering Chess and Shogi by Self-Play with a General Reinforcement Learning
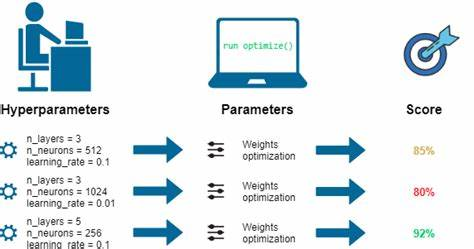
Information industry by wittx
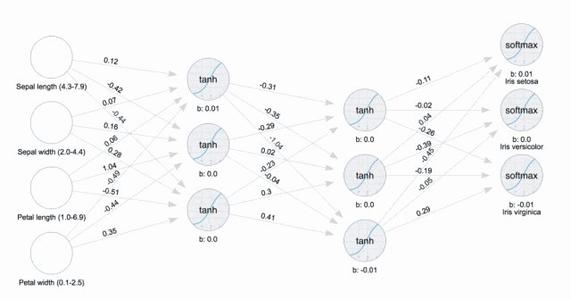
Information industry by wittx

Information industry by wittx

Information industry by wittx
Information industry by wittx

Information industry by wittx

Information industry by wittx
.jpg)
Information industry by wittx
Information industry by wittx
