
- Investment
- 科学论坛
-
Program
- Recruitment
- Center
News Message
SGD/AdaGrad/Adam deep learning 优化算法
- by wittx 2021-03-07
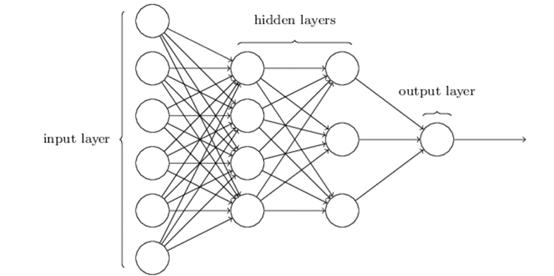
一个框架回顾优化算法
首先我们来回顾一下各类优化算法。
深度学习优化算法经历了 SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam 这样的发展历程。Google一下就可以看到很多的教程文章,详细告诉你这些算法是如何一步一步演变而来的。在这里,我们换一个思路,用一个框架来梳理所有的优化算法,做一个更加高屋建瓴的对比。
首先定义:待优化参数:
![[公式]](/images/download/1615107654498_37215.png) ,目标函数:
,目标函数: ![[公式]](/images/download/1615107655143_28707.png) ,初始学习率
,初始学习率 ![[公式]](/images/download/1615107655190_62086.png) 。
。而后,开始进行迭代优化。在每个epoch
![[公式]](/images/download/1615107655224_43427.png) :
:- 计算目标函数关于当前参数的梯度:
![[公式]](/images/download/1615107655263_34522.png)
- 根据历史梯度计算一阶动量和二阶动量:
![[公式]](/images/download/1615107655324_37906.png) ,
, - 计算当前时刻的下降梯度:
![[公式]](/images/download/1615107655425_28385.png)
- 根据下降梯度进行更新:
![[公式]](/images/download/1615107655483_29015.png)
掌握了这个框架,你可以轻轻松松设计自己的优化算法。
我们拿着这个框架,来照一照各种玄乎其玄的优化算法的真身。步骤3、4对于各个算法都是一致的,主要的差别就体现在1和2上。
SGD
先来看SGD。SGD没有动量的概念,也就是说:
![[公式]](/images/download/1615107655527_86055.png)
代入步骤3,可以看到下降梯度就是最简单的
![[公式]](/images/download/1615107655577_50708.png)
SGD最大的缺点是下降速度慢,而且可能会在沟壑的两边持续震荡,停留在一个局部最优点。
SGD with Momentum
为了抑制SGD的震荡,SGDM认为梯度下降过程可以加入惯性。下坡的时候,如果发现是陡坡,那就利用惯性跑的快一些。SGDM全称是SGD with momentum,在SGD基础上引入了一阶动量:
![[公式]](/images/download/1615107655621_95479.png)
一阶动量是各个时刻梯度方向的指数移动平均值,约等于最近
![[公式]](/images/download/1615107655681_60547.png) 个时刻的梯度向量和的平均值。
个时刻的梯度向量和的平均值。也就是说,t时刻的下降方向,不仅由当前点的梯度方向决定,而且由此前累积的下降方向决定。
![[公式]](/images/download/1615107655736_28377.png) 的经验值为0.9,这就意味着下降方向主要是此前累积的下降方向,并略微偏向当前时刻的下降方向。想象高速公路上汽车转弯,在高速向前的同时略微偏向,急转弯可是要出事的。
的经验值为0.9,这就意味着下降方向主要是此前累积的下降方向,并略微偏向当前时刻的下降方向。想象高速公路上汽车转弯,在高速向前的同时略微偏向,急转弯可是要出事的。SGD with Nesterov Acceleration
SGD 还有一个问题是困在局部最优的沟壑里面震荡。想象一下你走到一个盆地,四周都是略高的小山,你觉得没有下坡的方向,那就只能待在这里了。可是如果你爬上高地,就会发现外面的世界还很广阔。因此,我们不能停留在当前位置去观察未来的方向,而要向前一步、多看一步、看远一些。
NAG全称Nesterov Accelerated Gradient,是在SGD、SGD-M的基础上的进一步改进,改进点在于步骤1。我们知道在时刻t的主要下降方向是由累积动量决定的,自己的梯度方向说了也不算,那与其看当前梯度方向,不如先看看如果跟着累积动量走了一步,那个时候再怎么走。因此,NAG在步骤1,不计算当前位置的梯度方向,而是计算如果按照累积动量走了一步,那个时候的下降方向:
![[公式]](/images/download/1615107655783_17495.png)
然后用下一个点的梯度方向,与历史累积动量相结合,计算步骤2中当前时刻的累积动量。
AdaGrad
此前我们都没有用到二阶动量。二阶动量的出现,才意味着“自适应学习率”优化算法时代的到来。SGD及其变种以同样的学习率更新每个参数,但深度神经网络往往包含大量的参数,这些参数并不是总会用得到(想想大规模的embedding)。对于经常更新的参数,我们已经积累了大量关于它的知识,不希望被单个样本影响太大,希望学习速率慢一些;对于偶尔更新的参数,我们了解的信息太少,希望能从每个偶然出现的样本身上多学一些,即学习速率大一些。
怎么样去度量历史更新频率呢?那就是二阶动量——该维度上,迄今为止所有梯度值的平方和:
![[公式]](/images/download/1615107655841_70142.png)
我们再回顾一下步骤3中的下降梯度:
![[公式]](/images/download/1615107655887_27278.png)
可以看出,此时实质上的学习率由
![[公式]](/images/download/1615107655941_47459.png) 变成了
变成了 ![[公式]](/images/download/1615107655996_51463.png) 。 一般为了避免分母为0,会在分母上加一个小的平滑项。因此
。 一般为了避免分母为0,会在分母上加一个小的平滑项。因此![[公式]](/images/download/1615107656036_86246.png) 是恒大于0的,而且参数更新越频繁,二阶动量越大,学习率就越小。
是恒大于0的,而且参数更新越频繁,二阶动量越大,学习率就越小。这一方法在稀疏数据场景下表现非常好。但也存在一些问题:因为
![[公式]](/images/download/1615107656132_94234.png) 是单调递增的,会使得学习率单调递减至0,可能会使得训练过程提前结束,即便后续还有数据也无法学到必要的知识。
是单调递增的,会使得学习率单调递减至0,可能会使得训练过程提前结束,即便后续还有数据也无法学到必要的知识。AdaDelta / RMSProp
由于AdaGrad单调递减的学习率变化过于激进,我们考虑一个改变二阶动量计算方法的策略:不累积全部历史梯度,而只关注过去一段时间窗口的下降梯度。这也就是AdaDelta名称中Delta的来历。
修改的思路很简单。前面我们讲到,指数移动平均值大约就是过去一段时间的平均值,因此我们用这一方法来计算二阶累积动量:
![[公式]](/images/download/1615107656170_67809.png)
这就避免了二阶动量持续累积、导致训练过程提前结束的问题了。
Adam
谈到这里,Adam和Nadam的出现就很自然而然了——它们是前述方法的集大成者。我们看到,SGD-M在SGD基础上增加了一阶动量,AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来,就是Adam了——Adaptive + Momentum。
SGD的一阶动量:
![[公式]](/images/download/1615107656224_42354.png)
加上AdaDelta的二阶动量:
![[公式]](/images/download/1615107656284_62227.png)
优化算法里最常见的两个超参数
![[公式]](/images/download/1615107656339_25718.png) 就都在这里了,前者控制一阶动量,后者控制二阶动量。
就都在这里了,前者控制一阶动量,后者控制二阶动量。Nadam
最后是Nadam。我们说Adam是集大成者,但它居然遗漏了Nesterov,这还能忍?必须给它加上,按照NAG的步骤1:
![[公式]](/images/download/1615107656383_34158.png)
这就是Nesterov + Adam = Nadam了。
说到这里,大概可以理解为什么j经常有人说 Adam / Nadam 目前最主流、最好用的优化算法了。新手上路,先拿来一试,收敛速度嗖嗖滴,效果也是杠杠滴。
那为什么Adam还老招人黑,被学术界一顿鄙夷?难道只是为了发paper灌水吗?
请继续阅读:
Adam那么棒,为什么还对SGD念念不忘 (2)—— Adam的两宗罪
Adam那么棒,为什么还对SGD念念不忘 (3)—— 优化算法的选择与使用策略
————————————————————
补充:指数移动平均值的偏差修正
前面我们讲到,一阶动量和二阶动量都是按照指数移动平均值进行计算的:
![[公式]](/images/download/1615107656442_78034.png)
![[公式]](/images/download/1615107656557_11228.png)
实际使用过程中,参数的经验值是
![[公式]](/images/download/1615107656612_95221.png)
初始化:
![[公式]](/images/download/1615107656652_39600.png)
这个时候我们看到,在初期,
![[公式]](/images/download/1615107656695_57068.png) 都会接近于0,这个估计是有问题的。因此我们常常根据下式进行误差修正:
都会接近于0,这个估计是有问题的。因此我们常常根据下式进行误差修正:![[公式]](/images/download/1615107656730_15629.png)
![[公式]](/images/download/1615107656773_20247.png)
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=718

Best Last Month

Information industry by wittx

Information industry by wittx
Information industry by wittx

Information industry by wittx

Information industry by wittx
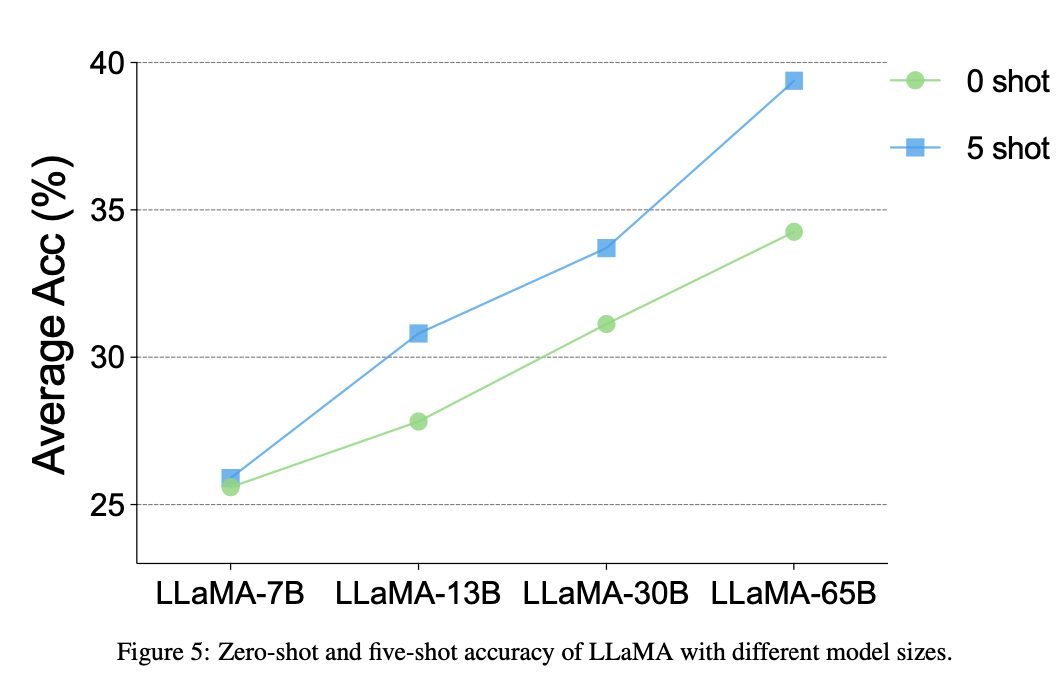
Information industry by wittxLLMs模型(GPTs、LaMDA、GLM/ChatGLM、PaLM/Flan-PaLM、BLOOM、LLaMA、Alpaca)

Information industry by wittx

Information industry by wittx

Information industry by wittx
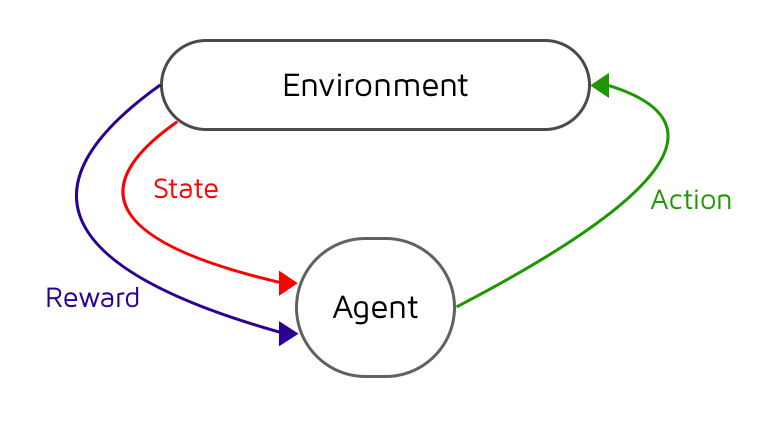
Information industry by AIMastering Chess and Shogi by Self-Play with a General Reinforcement Learning
