-
News Message
凸集，凸函数，凸优化问题，线性规划，二次规划，二次约束二次规
- by show 2021-02-15
1. 凸集的定义为：
其几何意义表示为：如果集合C中任意2个元素连线上的点也在集合C中，则C为凸集。其示意图如下所示：
常见的凸集有：
n维实数空间；一些范数约束形式的集合；仿射子空间；凸集的交集；n维半正定矩阵集；这些都可以通过凸集的定义去证明。
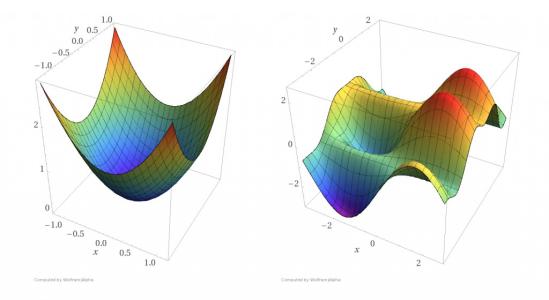
2. 凸函数的定义为：
其几何意义表示为函数任意两点连线上的值大于对应自变量处的函数值，示意图如下：
凸函数的一阶充要条件为：
其中要求f一阶可微。
二阶充要条件为：
其中要求f二阶可微，表示二阶导数需大于0才是凸函数。
常见的凸函数有：指数函数族；非负对数函数；仿射函数；二次函数；常见的范数函数；凸函数非负加权的和等。这些可以采用上面2个充要条件或者定义去证明。
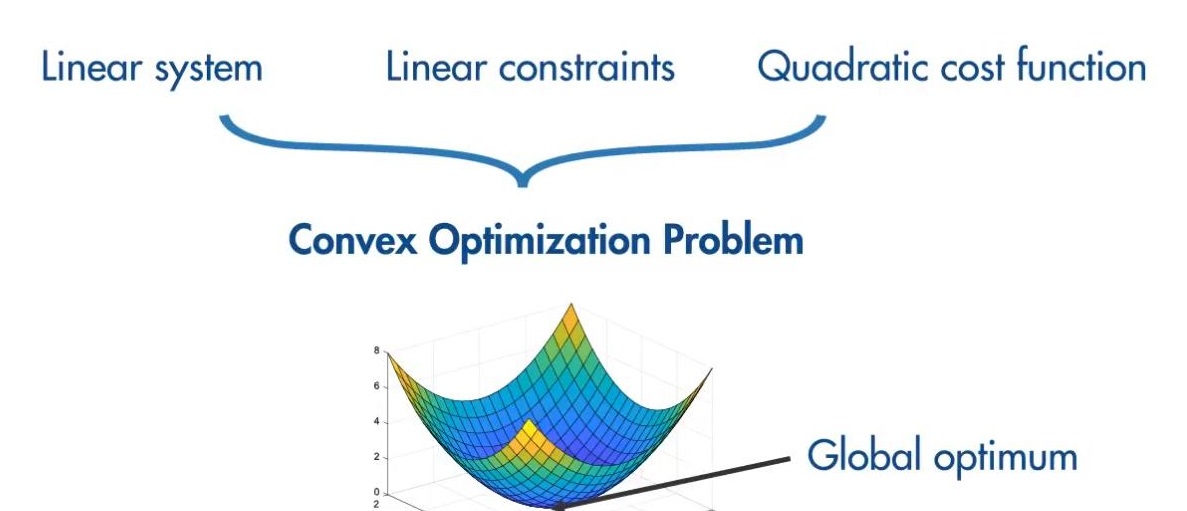
3. 凸优化问题（OPT）的定义为：
凸优化有个非常重要的定理，即任何局部最优解即为全局最优解。
凸优化，或叫做凸最优化，凸最小化。研究定义于凸集中的凸函数最小化的问题。它要求目标函数是凸函数，变量所属集合是凸集合的优化问题。或者目标函数是凸函数，变量的约束函数是凸函数（不等式约束时），或者是仿射函数（等式约束时）。（凸优化就是：1、在最小化（最大化）的要求下，2、目标函数是一个凸函数（凹函数），3、同时约束条件所形成的可行域集合是一个凸集。以上三个条件都必须满足。而世间万物千变万化，随便抽一个函数或集合它都可能不是凸的。）
对于凸优化问题来说，局部最优解就是全局最优解。
所以凸优化为什么重要？——凸优化性质好，并且即使是日常生活中的许多非凸优化问题，目前最有效的办法也只能是利用凸优化的思路去近似求解。（1、还是有相当一部分问题是或等价于凸优化问题。2、大部分凸优化问题解起来比较快，也即多项式时间可解问题（P）。3、很多非凸优化或NP-Hard的问题可以转化（并非是等价的）为P的凸优化问题。并给出问题的界或近似。）
常见的凸优化问题包括：有许多问题都可以直接建立成凸优化模型（比如：线性规划LP（Linear Programming）、某些特殊的二次规划QP（Quadratic Programming）、锥规划CP（Conic Programming）其中包括：要求约束中变量落在一个二阶锥里的二阶锥规划SOCP（Second Order Cone Programming）、要求约束中变量是半正定矩阵的半定规划SDP（Semi-Definite Programming）等）。以上这些类型，总之就是要符合凸优化上述的要求。需要说明的就是，许多可行域都可以看作是凸锥（Convex Cone）的交集，所以将以上一些类型的约束混合起来，依然是凸优化问题。
4. 二次规划（QP）：该问题是优化下面的式子：
5. 二次约束的二次规划（QCQP）：该问题是优化下面的式子：
参考： http://cs229.stanford.edu/section/cs229-cvxopt.pdf
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=697
Best Last Month
Information industry by wittx
Computer software and hardware by wittx
Information industry by wittx3D nanofabricated soft microrobots with super-compliant picoforce springs as onboard sensors and act
Information industry by wittxChameleon: Plug-and-Play Compositional Reasoning with Large Language Models
.jpg)
Information industry by wittx
Information industry by wittx
Information industry by wittxRelationship between thermoelectric figure of merit and energy conversion efficiency
Information industry by wittx
Information industry by wittx
Information industry by wittx
