2019 开源论文：基于图神经网络的协同过滤算法--Intelligent technology investment network-上海优钧机械设备科技

News Message

2019 开源论文：基于图神经网络的协同过滤算法

by wittx 2020-10-10

论文：https://www.paperweekly.site/papers/3212
源码：xiangwang1223/neural_graph_collaborative_filtering

引言

协同过滤作为一种经典的推荐算法在推荐领域有举足轻重的地位。协同过滤（collaborative filtering）的基本假设是相似的用户会对物品展现出相似的偏好。

总的来说，协同过滤模型主要包含两个关键部分：1）embedding，即如何将 user 和 item 转化为向量表示；2）interaction modeling，即如何基于 user 和 item 的表示来重建它们的历史交互。

传统协同过滤算法（如经典的矩阵分解和神经矩阵分解）本质还是给 user 和 item 初始化一个 embedding，然后利用交互信息来优化模型。它们并没有把交互信息编码进 embedding 中，所以这些 embedding 都是次优的。

直观地理解，如果能将 user-item 的交互信息编码进 embedding 中，将提升 embedding 的表示能力进而提升模型的预测能力。本文的主要创新点在于利用二部图神经网络将 User-Item 的历史交互信息编码进 Embedding 进而提升推荐效果。更重要的是，本文显式地考虑 User-Item 之间的高阶连接性来进一步提升 embedding 的表示能力。

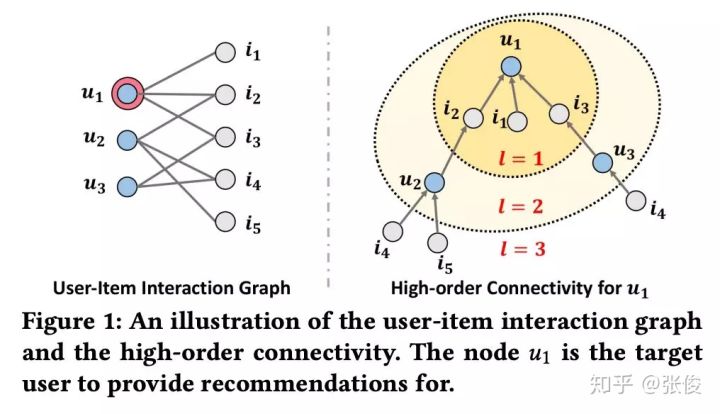
图 1 展示了一个 user-item 的二部图及 $u_{1}$ 的高阶连接性。 $u_{1}$ 的高阶连接性表示 $u_{1}$ 通过长度大于 1 的路径连接到的节点。例如， $u_{1}$ 通过长度 l=2 的路径连接到 $u_{2}$ 和 $u_{3}$ ，这代表 $u_{1}$ 的 2 阶连接性； $u_{1}$ 通过长度 l=3 的路径连接到 $i_{4}, i_{5}$ ，这代表 $u_{1}$ 的 3 阶连接性。需要注意的是，虽然 $i_{4}$ 和 $i_{5}$ 都是 $u_{1}$ 的 3 阶邻居，但是 $i_{4}$ 可以通过更多的路径连接到 $u_{1}$ ，所以 $i_{4}$ 与 $u_{1}$ 的相似度更高。

模型

模型主要分为 3 个部分：1）Embedding Layer：将 user 和 item 的 ID 映射为向量表示；2）Embedding Propagation Layers：将初始的 user 和 item 表示基于图神经网络来更新；3）Prediction：基于更新后的 user 和 item 表示来进行预测。模型架构图见 Figure 2。

Embedding Layer

这里对 User 和 Item 分别初始化相应的 Embedding Matrix，然后通过 User 或者 Item 的 ID 进行 Embedding Lookup 将它们映射到一个向量表示。

注意，这里初始化的 Embedding 可以认为是 0 阶表示，即：

Embedding Propagation Layers

受 GNN 的 message-passing 架构的启发，NGCF 针对 User-Item 二部交互图设计了 Embedding Propagation 来学习 User 和 Item 的表示。这里作者首先详细的描述了一阶传播，然后泛化到高阶传播。

一阶传播主要包含：消息构建和消息聚合。给定(u,i)，从 i 传播到 u 的消息 $m_{u \leftarrow i}$ 可以定义为：

其中， $W_{1},W_{2}\in R^{d'\times d}$ 都是可学习的参数矩阵， $N_{u}$ 和 $N_{i}$ 分别代表 u 和 i 的度。这里 $1/\sqrt{\left| N_u \right|\left| N_i \right|}$ 可以理解为归一化系数。

基于上面构建的消息，下一步就是聚合消息来更新节点表示：

其中， $e_{u}^{(1)}$ 代表经过 1 次聚合之后的节点表示。因为单层的消息聚合只能聚合 1 阶邻居的信息，所以这里实际代表了 u 的一阶表示。需要注意的是，这里除了聚合邻居的信息，更重要的是考虑节点自身的信息 $m_{u\leftarrow u}=W_{1e_{u}}$ 。

高阶传播实际就是将上述的一阶传播堆叠多层。这样经过 l 次聚合，每个节点都会融合其 l 阶邻居的信息，也就得到了节点的 l 阶表示 $e_{u}^{(l)}$ 。

Figure 3 清晰地展示了如何在高阶传播中融合高阶邻居的信息。

上面的传播过程也可以写成矩阵的形式，这样在代码实现的时候可以高效的对节点 Embedding 进行更新。

其中， $E^{(l)}\in R^{(N+M)\times d_{l}}$ 是 l 阶的 user 和 item 的表示， $R\in R^{N\times M}$ 是 user-item 交互矩阵，D 是对角度矩阵。

Model Prediction

模型的预测非常简单，将 L 阶的节点表示分别拼接起来作为最终的节点表示，然后通过内积进行预测。

实际这里采用了类似 18 ICML Representation Learning on Graphs with Jumping Knowledge Networks 的做法来防止 GNN 中的过平滑问题。GNN 的过平滑问题是指，随着 GNN 层数增加，GNN 所学习的 Embedding 变得没有区分度。过平滑问题与本文要捕获的高阶连接性有一定的冲突，所以这里需要在克服过平滑问题。

最终的损失函数就是经典的 BPR 损失函数：

实验

本文在 Gowalla、Yelp2018 和 Amazon-Book 上进行了大量实验来回答以下 3 个问题：

和 state-of-the-art 的方法相比，NGCF 的效果如何？
模型对于超参数（如模型层数，dropout）的敏感性。
高阶连接性对于模型的影响。

本文的 baseline 主要可以分为两大类：非图神经网络的推荐算法（如 MF 和 CMN）和基于图神经网络的推荐算法（PinSage 和 GC-MC）。实验效果如 Table 2 所示：

可以看出，本文所提出的 NGCF 优势很明显，尤其是在 recall 上的提升均超过 10%。同时，作者还对数据进行了稀疏化并进一步验证来说明 NGCF 来稀疏数据上的优势。

从 Figure 4 可以看出，NGCF 在数据稀疏度较高的时候有明显优势，随着稀疏度的下降，NGCF 的优势越来越小甚至被 baseline 超过了。

另外，作者验证了模型层数、卷积形式和 dropout 对 NGCF 的影响，具体见 Table 3、Table 4 和 Figure 5。

最后，作者研究了高阶连接性对 NGCF 的影响，如 Figure 6 所示。

注意这里 MF 可以看做是 NGCF-0。可以看出，随着阶数的增加，相同颜色的节点更好的聚集在一起。也就是说，高阶连接性确实有助于学习 User 和 Item 的 Embedding。

结论

本文提出了基于图神经网络的协同过滤算法 NGCF，它可以显式地将 User-Item 的高阶交互编码进 Embedding 中来提升 Embedding 的表示能力进而提升整个推荐效果。NGCF 的关键就在于 Embedding Propagation Layer 来学习 User 和 Item 的 Embedding，后面的预测部分只是简单的内积。可以说，NGCF 较好地解决了协同过滤算法的第一个核心问题。另外，本文的 Embedding Propagation 实际上没有考虑邻居的重要性，如果可以像 Graph Attention Network 在传播聚合过程中考虑邻居重要性的差异，NGCF 的效果应该可以进一步提升。