量子计算机工作原理--Intelligent technology investment network-上海优钧机械设备科技

News Message

量子计算机工作原理

by wittx 2020-10-06

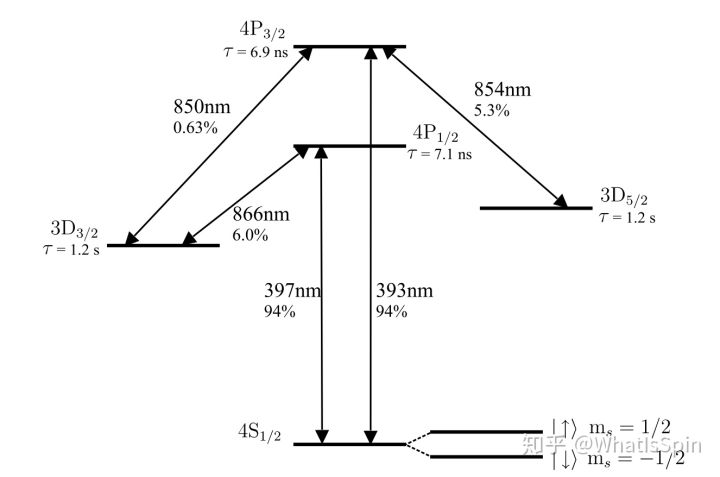
量子计算机工作原理

介绍一下基于离子阱技术实现的量子计算机，以Grover算法为例，说明量子计算机的优越性。
1 粒子的自旋
任何一个粒子(原子，光子，离子，电子等等)都有自旋，自旋有两个方向，上旋 (Spin Up) 或者下旋 (Spin Down)。除此之外没有其他方向，比如不能是斜向上45度。注意这里的上旋或者下旋并不是说粒子真的在旋转，而是其外在表现类似经典力学中的自转。还是用Wiki的话吧
在量子力学中，自旋（英语：Spin）是粒子所具有的内禀性质，其运算规则类似于经典力学的角动量，并因此产生一个磁场。虽然有时会与经典力学中的自转（例如行星公转时同时进行的自转）相类比，但实际上本质是迥异的。经典概念中的自转，是物体对于其质心的旋转，比如地球每日的自转是顺着一个通过地心的极轴所作的转动。
2 量子数
为了更好的理解上旋和下旋，我这里简单介绍一下施特恩－格拉赫实验，但在此之前先介绍一下量子数 (quantum number)，补充一下基础知识。
学过高中化学都知道，电子围绕着原子核旋转，每个电子都有自己的轨道，这些轨道按照Energy Level划分为 $n=1,2,3,\dots$ 原子最多可以有两个Level = 1的电子，8个Level = 2电子，依此类推。这里的Energy Level $n=1,2,3,\dots$ 称为principal quantum number (主量子数)
然而这些轨道按照形状划分又可以有好多种，比如最简单的球形(circle)简记为s，下图左1；极形(polar)简记为p,下图中；苜蓿叶形(cloverleaf)简记为d, 下图右，当然有更复杂的形状这里就不列出了。用角量子数(angular quantum number) $l=0,1,2,\dots$ 表示不同形状。也有称为轨道量子数(orbital quantum number)的
角量子数l=0,1,2代表了轨道的形状
同一形状的轨道会有不同方向，比如polar形轨道会有3个方向，分别沿着x轴，y轴和z轴，如下图所示。
polar形轨道有3个不同的方向 m= -1, 0, +1 (放大可看清里面的电子运动) https://www.youtube.com/watch?v=BzHFBBD-hb4
这三个方向分别用magnetic quantum number(磁量子数) $m=-1,0,+1$ 表示。
而cloverleaf形轨道有5个方向，用 $m=-2,-1,0,1,2$ 表示，如下图所示
cloverleaf形轨道有5个不同的方向, 分别标记为m = -2, -1, 0, +1, +2
下面是是量子数的组合规则
角量子数 (l) 可以取 0 到 n - 1. 之间的任意数字。比如 n = 3, 那么 l 可以取0, 1, 或者 2.
磁量子数 (m) 可以取 -l 到 +l之间的任意数。比如 l = 2, 那么m 可以取 -2, -1, 0, +1, 或者 +2.
同一个形状同一个方向的轨道拥有最多容下2个电子。比如s形轨道，只有一个方向，可以容2个电子，而p轨道有3个方向，可容6个电子，d可容10个电子，f可容14个电子，等等。
来看看具体的例子吧：
$\begin{eqnarray} \mathrm{Atom}&\quad & \mathrm{Configuration}\\ \mathrm{H}&\quad & \ 1s^1\\ \mathrm{He}&\quad & \ 1s^2 = \mathrm{[He]}\\ \mathrm{Li}&\quad & \ \mathrm{[He]}2s^1\\ \mathrm{Be}&\quad & \ \mathrm{[He]}2s^2\\ \mathrm{B}&\quad & \ \mathrm{[He]}2s^22p^1\\ \mathrm{C}&\quad & \ \mathrm{[He]}2s^22p^2\\ \mathrm{N}&\quad & \ \mathrm{[He]}2s^22p^3\\ \mathrm{O}&\quad & \ \mathrm{[He]}2s^22p^4\\ \mathrm{F}&\quad & \ \mathrm{[He]}2s^22p^5\\ \mathrm{Ne}&\quad & \ \mathrm{[He]}2s^22p^6 = \mathrm{[Ne]}\\ \mathrm{Na}&\quad & \ \mathrm{[Ne]}3s^1\\ \mathrm{Mg}&\quad & \ \mathrm{[Ne]}3s^2\\ \mathrm{Al}&\quad & \ \mathrm{[Ne]}3s^23p^1\\ \mathrm{Si}&\quad & \ \mathrm{[Ne]}3s^23p^2\\ \mathrm{P}&\quad & \ \mathrm{[Ne]}3s^23p^3\\ \mathrm{S}&\quad & \ \mathrm{[Ne]}3s^23p^4\\ \mathrm{Cl}&\quad & \ \mathrm{[Ne]}3s^23p^5\\ \mathrm{Ar}&\quad & \ \mathrm{[Ne]}3s^23p^6 = \mathrm{[Ar]}\\ \mathrm{K}&\quad & \ \mathrm{[Ar]}4s^1\\ \mathrm{Ca}&\quad & \ \mathrm{[Ar]}4s^2\\ \dots & & \dots \end{eqnarray}$
比如 $\mathrm{Be} = \ \mathrm{[He]}2s^2$ ，表示Be原子1s形轨道(Energy Level = 1, 形状s)拥有2个电子, 2s形轨道也拥有2个电子.
参考文献 (https://chemed.chem.purdue.edu/genchem/topicreview/bp/ch6/quantum.php)
3 施特恩－格拉赫实验
啰里巴嗦了一堆，现在终于可以解释施特恩－格拉赫实验了。
施特恩－格拉赫实验
如图所示，通过炉子加热银原子，然后发射出去，银原子从炉子中穿出经过非均匀磁场后打在屏上，屏可以显示银原子的位置。那么根据经典理论，在屏幕上我们应该看到连续的线 (Classical Prediction)。(加热银原子是为了方便最后胶片感光找位置)
先来解释一下为什么是连续的线。来观察一下银原子，如下图，银原子有47个电子，其中内部46个电子对称，正负抵消，不会受磁场影响。最外层的电子运行轨道是球形。
银原子的电子分布
因此整个原子的角动量取决于最外侧电子的绕核运动所产生的轨道角动量。经典理论认为，这一角动量可以是任意方向，而且连续的。运动的电子产生磁场，也就形成了磁矩。整个原子可以看作是一个吸铁石，有N/S两极。在均匀的磁场中，运动的吸铁石不会发生偏转，因为N/S极受力相等，也就抵消了。但是如果是逐渐增强的磁场，而且N极稍微靠前，则整个吸铁石就会向底部偏转，因为N极受力大。如果是S极靠前，则会向上偏转。最后的结果是一堆原子在屏幕上形成一条线。原子的偏移取决于N/S极摆放的角度。
然而事实的情况是，屏幕上只有两个点。那么这该怎么解释？
既然位置是离散的，那么首先要求最外的电子没有轨道角动量，否则位置必须连续。电子绕着原子核旋转，怎么会没有角动量呢？应该这么理解，电子本身并没有运动，而是等概率出现在轨道各个位置上。由于轨道是球面因此这个电子角动量为0。没有角动量也就不受外界磁场的影响(http://hyperphysics.phy-astr.gsu.edu/hbase/spin.html#c6)。
其次，必须有其他的角动量来提供这个偏移。那只能是电子的自旋了，而且自旋方向只有两个，要么彻底上，要么彻底下。严格来说取决于磁场的摆放，如果磁场横着摆，那么自旋方向要么左，要么右。
只有最外面的电子提供的自旋角动量，内部的46个电子是没有贡献他们的自旋角动量的，否则值就是离散的多个点，而不是两个点了。为了解释为什么内部的电子自旋角动量为0，我们对前面电子分布作一个补充，前面提到，同一energy level，同一形状轨道的一个方向最多容纳两个电子，而且这两个电子的自旋方向是相反的（泡利不相容原理），相互抵消了。
4 叠加态
SO, WHAT IS SPIN?
这个问题至今没有搞清楚。但这不影响我们理解量子计算的原理。
前面我们提到自旋分向上和向下两个方向。但究竟是哪个方向只有在测量的时候才知道，比如前面的银原子，其外层电子的自旋方向只有在进入磁场测量时才定下来。我们用量子比特 $\mathrm{qubit} = |0\rangle$ 表示下旋， $\mathrm{qubit} = |1\rangle$ 表示上旋。测量时，量子比特以概率p处于状态0，概率1-p处于状态1. 这可以用bloch 球表示，如下图。 (这个图中用0表示上旋，1表示下旋，但这不影响我们的理解)
bloch 球
测量前，量子比特的状态可以用球面任意一点表示，夹角代表了测量后的概率，关系为 $p(0) = \cos^2 (\theta/2), \quad p(1) = 1- p(0)$ , $\varphi$ 代表了相位
我们可以用下面的式子表示测量前的状态
$| \psi \rangle = \alpha |0 \rangle + \beta |1\rangle$
其中 $\alpha = \cos(\theta/2), \ \beta = e^{i \varphi} \sin(\theta/2)$ 为复数。 $\alpha , \beta$ 满足绝对值平方和为1
$|\alpha|^2 + |\beta|^2 = 1$
量子比特处于0的概率为 $p(0) = |\alpha|^2$ , 1的概率为 $p(1) = |\beta|^2$
有时候也用向量的形式表示
$| \psi \rangle = \left[\begin{array}& \alpha \\ \beta \end{array}\right]$
5 基态和激发态以及状态转换
实现量子比特有很多方法，离子阱是很常见的一种。在此之前，先科普一下原子的基态和激发态。这是为了之后更好地理解冷却技术以及Raman效应。
下图显示了氢原子的基态和激发态，其中的n就是之前提到的principle quantum number，代表了轨道的Energy Level. 平常条件下，电子处于能量最低的level, n = 1。这一状态称为基态。当电子受到外界的能量，比如激光照射，则电子会从轨道n = 1跃迁到 n =2或者更高。这一状态称为激发态。激发态并不是稳定的状态，电子会落回到最低的轨道，并发出红色、蓝绿色或是其他的不可见光。
氢原子的基态和激发态
具体来说，怎么用激光把基态变为激发态呢？
熟悉光电效应的朋友都知道，光的能量取决于光的频率。用特定频率的光照射电子，当电子吸收了光子后，就会得到想要的激发态。跃迁到高Level需要越高的能量，也就需要更高的频率。反之当原子从激发态退回到基态，也会释放出相应频率的光。如下图所示，蓝光频率>绿光>红光
原子可以自发地退回到基态，此时原子会向随机方向射出一个特定频率的光子，频率相当于从基态跃迁到激发态所需光子的频率，这个过程称为spontaneous emission。还有一种办法是可控的让原子退回基态，做法是向电子射入一个光子，其频率等于该电子从基态跳跃到当前激发态所需光子的频率。而此时电子会沿着射入的方向射出两个该频率的光子，并退回到基态。这个过程称为 stimulated emission. 如下图所示
stimulated emission
为了控制原子的状态，我们必须敢在spontaneous emission之前用stimulated emission将原子退回到我们想要的基态。这就要求spontaneous emission越迟越好，原子自我维持激发态的状态时间越长越好。
并不是任意的两个状态都可以转换，电子从一个轨道跳跃到另一个轨道必须满足选定规则(Selection Rule)。可以转换的状态称为Allowed Transition，否则称为Forbidden Transition。（严格来说不是不能转，而是概率很小）
选定规则具体来说有这么三条：
$\Delta n \in \mathrm{Any\ Number}$
$\Delta l \in \{-1, +1\}$
$\Delta m \in \{-1, 0, +1\}$
这里的 $n, l, m$ 就是之前所说的三个量子数，分别代表了轨道的能级、形状和电子运动方向)
举个栗子，比如一个电子的量子数为 $n =2, l = 1, m = -1$ ，即轨道的Energy Level = 2, 形状是p, 方向沿着x轴，这个电子可以跃迁到到 $n = 1, l = 0, m = 0$ 的轨道上，因为满足选定规则。但是它不能跃迁到 $n =2, l = 1, m = 0$ ，因为 $\Delta l = 0$ 不满足选定规则。
6 钙离子Ca+的状态转换
现在我们要选择离子，及其两个状态作为 $|0\rangle$ 和 $|1\rangle$
可以选用钙离子。首先把钙原子加热到800摄氏度，形成蒸汽，然后用电子流轰击，将钙原子最外层的一个电子赶走，这样最外层只剩一个电子，从而形成了带一个正电荷的钙离子，这样就方便后面的离子阱固定了。为什么要选择钙？这是因为钙离子最外层只有一个电子，方便实现轨道的跃迁。
此时的钙离子的电子分布如下图所示
Ca+离子的电子分布
还记得之前提到的嘛？s轨道有1方向，最多容纳2个电子，p轨道有3个方向，可容6个电子，等等。这个图左侧给出了电子的分布可以看到最外层轨道只有一个电子，我们就是要控制它的跃迁来实现状态转移。这个电子的轨道量子数为 (轨道形状是s)
根据之前的选定规则，最外层电子可以跃迁到如下的状态：
Ca+最外层电子的Allowed Transition https://www2.physics.ox.ac.uk/sites/default/files/JHomethesis.pdf
这个图里出现很多新符号，还有一些疑问。我们这里要先解释一下。首先 $4P_{1/2}$ 这里的1/2是Total angular momentum quantum number记作 $j$ . 这个分数是由于spin引起的。之前的施特恩－格拉赫实验证实了电子有自旋，那就有角动量，称为Spin Quantum Number (https://en.wikipedia.org/wiki/Spin_quantum_number) ，根据其两个方向标记为 $m_s=\pm1/2$ , 其加上角量子就得到了Total angular momentum quantum number，且不能为负数:
$j= m_s + l, j > 0$
为什么这么定义呢？这是为了计算总角动量用的。简单点说，总角动量=轨道角动量+自旋角动量，当这两个方向相同，自旋取正号，相反，自旋角动量取负号。而球形轨道s没有轨道角动量，因此直接取自旋角动量的绝对值。
这个图中还有个问题，为什么左边的3D在4S之上？那是因为3D轨道比4S能量高。关于这点可以参考下图。
不同轨道的Energy
7 用Hyperfine Structure制备|0》|1》
电子有上旋或者下旋，同样质子也有。旋转的质子产生磁场，而旋转的电子在磁场中会有磁矩，这样质子和电子就产生了相互作用，也就产生了势能。当电子质子同向自旋的时候(parallel)，会有势能E2，当电子和质子反向旋转的时候，会有势能E1。E2 > E1。其差别很小。下图显示了氢原子的这两种情况。
当一堆处于激发态的氢原子，他们处于 $2P_{1/2}$ 或是 $2P_{3/2}$ 的激发态，当他们衰退回基态 $1S_{1/2}$ 的时候，会释放一个光子，由于能量不同，这些光子具有不同频率，在胶片上会显示出不同的条纹，如下图所示。
Fine Structure of Hydrogen
对于一般的原子来说，电子的自旋和原子核的自旋也会想作用，产生能量。这种结构称为Hyperfine Structure
Hyperfine structure 非常稳定，不容易受到外界的磁场的影响。因此可以用来制备状态 $|0\rangle, |1\rangle$ ，比如可以用钙离子Ca+的 $4S_{1/2}, m_s=-1/2$ 作为 $|0\rangle$ ， $4S_{1/2}, m_s = 1/2$ 作为 $|1\rangle$
状态|0》和状态|1》
8 离子阱
为了方便对量子操作，首先要固定它。首先，把离子放在一个真空的缸中，然后用3束激光去冷却这个离子，使它的能量处于最低状态。
常用的是Paul Trapping，具体来说就是下面这个东西。一个环加上上下两个电极，上下两个电极对准环中心。看到中间那个小点了嘛？那就是被Trap住的离子。具体来说这玩意是这么操作的，一开始上下两个电极带正电，环带负电。由于离子是正电，因此离子向环靠拢，而远离上下两个电极。然后改变电极，上下电极负电，环带正电，这样离子就开始远离环而向上或者下电极靠拢。如此反复改变电极的正负，离子就在环中心荡来荡去，跑不了了。
Paul Trapping
为什么不用一圈正电极把离子约束在中央呢？根据Earnshaw's theorem，离子是不可能被静止的电极固定住的。
9 多普勒冷却
离子阱只是把离子固定住，要让离子以概率1保持在低能量状态，还需要冷却技术。所谓冷却就是限制离子的震动，因为这些震动会产生温度，是得电子发生不必要的跃迁。
常用的有多普勒冷却，其原理是多普勒效应。所谓多普勒效应就是当我们向着波源的方向运动，波的频率会变高，而背着波源的方向运动，波的频率会变低。比如当火车向我们驶来的时候，火车的鸣笛刺耳，火车驶过，背着我们远去的时候，鸣笛就会低沉。就是这个道理。
电子只吸收特定频率的光子，假设只吸收蓝光。我们对着电子发射一束绿光，如果电子静止，则绿光不能被电子吸收，也就不能改变电子的运动状态。如果电子背离光运动，光的频率相对电子会变低，变为红光，也不能被吸收。而如果电子向着光源运动，则光频率会变高，变成蓝光，被电子吸收了。根据动量守恒，电子会变慢。处于激发态的电子还会自发射出光子从而退回到基态。虽然射出的光子是随机方向的，但由于会射出很多光子，平均下来就是0动量了。
多普勒冷却原理
多普勒冷却不足以制造足够低的温度，还有其他冷却方法可以获取更低的温度，比如Optical pumping, Resolved-sideband cooling, Raman Cooling。每个方法背后都是一大堆知识点，我只求理解大意，没细看这些东西，总之相当相当的复杂！！
到此为止，我们就算能把离子搞定在0状态了！
10 Hadamard Gate
很多算法，包括这里要讲的Grover算法，需要完全随机的初始状态，即1/2概率0状态，1/2概率1状态。 Hadamard Gate可以做到这一点：简而言之，就是把一个确定的状态搞成不确定的，但再加上一个Gate又把不确定的还原成愿状态：
$|0\rangle \stackrel{\mathrm{hadamard}}{\rightarrow} \frac{|0\rangle + |1\rangle }{\sqrt 2}\stackrel{\mathrm{hadamard}}{\rightarrow} |0\rangle$
$|1\rangle \stackrel{\mathrm{hadamard}}{\rightarrow} \frac{|0\rangle - |1\rangle }{\sqrt 2}\stackrel{\mathrm{hadamard}}{\rightarrow} |1\rangle$
用矩阵表示就是,对于量子比特 $q = \left[\begin{array}& \alpha \\ \beta \end{array}\right]$
$Hq = \frac{1}{\sqrt{2}}\left[\begin{array} & 1 & 1\\ 1 & -1 \end{array}\right]\left[\begin{array}&\alpha \\ \beta \end{array}\right]$
这个东西怎么做的我还没看懂。这里先贴一个链接 An approach to realize a quantum Hadamard gate through optical implementation，以后看懂了再补充
之前处于0状态的量子比特经过Hadamard Gate 变成完全随机的了。我们可以制作多个这样的量子比特作为Grover算法的输入
Hadamard Gate是一个很重要的单比特门，输入一个qubit，输出一个qubit，除了初始化，它在后面还有很大的用处，算是链接量子计算各个逻辑门的血液。因为它这样重要的性质：对任何量子比特，连续经过两个Hadamard Gate就可以恢复到原来状态，
$H H q = q$
11 控制非门(CNOT Gate)
CNOT Gate是另一个非常重要的门，它是量子计算机超越经典计算机的关键所在。
CNOT Gate输入是两个量子比特 $|ab\rangle$ ，输出也是两个qubit。如果 $a$ 处于0状态，那么 $b$ 不变，否则 $b$ 交换0和1的概率:
$\alpha |00\rangle + \beta |01\rangle + \delta |10\rangle + \gamma |11\rangle \stackrel{\mathrm{CNOT}}{\rightarrow}\alpha |00\rangle + \beta |01\rangle + \gamma |10\rangle + \delta |11\rangle$
用矩阵表示
$\left[\begin{array} & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array}\right]\left[\begin{array} &\alpha \\\beta\\ \delta \\ \gamma \end{array}\right] = \left[\begin{array} &\alpha \\\beta\\ \gamma \\ \delta \end{array}\right]$
为什么说CNOT Gate这么关键呢？如果我们制备2个qubit ，这两个qubit之间是没有任何关系的，因此测量结果是独立的: $p_{ab}(xy) = p_a(x) p_b(y)$ 用矩阵表示联合分布：
$\left[\begin{array} & pq &p(1-q) \\ (1-p)q & (1-p)(1-q)\end{array}\right]$
其中 $p=p_a(0), q=p_b(0)$
经过CNOT Gate之后，联合概率变为
$\left[\begin{array} & pq &p(1-q) \\ (1-p)(1-q) & (1-p)q\end{array}\right]$
这样的联合分布就不能分解成两个独立分布了。举个栗子，假设 $p=0.5, q=1$ 那么上面的矩阵变为
$\left[\begin{array} & 0.5 & 0 \\ 0 & 0.5\end{array}\right]$
这个联合概率分布是不能分解成两个独立分布的乘积的。否则我们从第一行我们得到，第一个量子成为状态1的概率为0，而从第二行第二列，可以推出第一个量子成为1的概率不为0，矛盾。
独立制备的n个量子比特，由于独立分布，他们的联合概率分布可以只需要用n个数字描述。但CNOT Gate打破了量子比特之间的独立性，这就提供了一种可能：刻画他们的联合概率分布需要 $2^n$ 个数字。也就是说n个量子比特可以表示一个任意 $2^n$ 维的向量，通过操作这n个量子比特从而达到操作 $2^n$ 维向量的目的。量子算计机可以实现任意的对 $2^n$ 维向量的幺正变换：
$v\stackrel{量子计算}{\rightarrow}Uv, U是任意酉阵, v是2^n维向量$
这是因为CNOT Gate的很重要的一个性质：通过组合多个CNOT Gate可以实现任意的幺正变换:
$v\stackrel{\mathrm{CNOT\ Gate}组合}{\rightarrow}Uv$
关于这点，这篇文章讲的很好 https://zhuanlan.zhihu.com/p/21367507 ，这里就不展开叙述了。之后遇到需要再具体阐述。
12 量子谐振子
下面介绍一下CNOT Gate的物理实现，在此之前必须先介绍一下量子谐振子(Quantum Harmonic Oscillator)。
双原子分子中，原子的震动就像用弹簧拉着的两个球一样。比如氢分子通过共价键(Covalent Bond)连接两个原子。这个弹簧系统会有势能V，它是关于原子距离的一个函数V(r)。
共价键连接两个氢原子
现在我们来看看V(r)是怎样的一个函数。根据拉格朗日力学，一个惯性系统中的总能量等于动能加上势能。这里的动能就是氢原子的振动的能量，而势能则是V(r)。我们考虑一下几个点：
对氢气加热，使得氢原子剧烈震动，动能加大，直到最后分离。这种情况下弹簧断裂，也说明了分的很远的原子的势能不是无限的，足够的动能就能使原子分的更开。所以 $V( \infty ) = C$ ，是一个常量。
把两个氢原子死死压在一起，比如氢气压缩成液体，液态氢温度很低，所以动能减小，势能增大。但却不能无限压缩，这说明让两个氢原子重合是不可能的：氢原子速度为0，势能无限大。 $V(0) = \infty$
在常温下，氢分子保持气态，既不会被拆成原子，也不会压缩成液体。这说明此时V(r)最小
这样我们就得到了V(r)的曲线,
双原子分子势能V(r)曲线，r0时V(r)最小，比如常温下的稳定状态，来源: https://www.youtube.com/watch?v=Thy9YXnAY2s
我们不关心r很大的情况，因此可以用一个二次函数来近似V(r), 比如上图中的蓝色抛物线。
所以双原子分子中原子有一个平衡距离，小于这个距离，两个原子互相排斥，否则互相吸引。在量子力学中，这个系统的势能是离散的，如下图所示,x轴表示两个原子的距离，在x0处达到最小。图中的 $n=0,1,2,\dots$ 称为振动能级(Vibrational Energy Level)
双原子分子的势能随距离变化的函数,来源: http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hosc.html
这种多原子的弹簧系统称为量子谐振子。通过对双原子系统中的一个原子施力，使它远离或者靠近另一个原子，那么该原子的动能传递到另一个原子，而自己的动能消失，然后再将动能传回该原子，如此反复。这就好比两个连通的单摆一样，如下面的动画。这种弹簧可以基于共价键，也可以基于库仑力，用于连接粒子，比如这里的Ca+离子。至于库仑力是怎么做成弹簧的，我查到的文献说:"secret recipe".
连通的单摆传递动能 https://www.youtube.com/watch?v=v1_-LsQLwkA
振动能级跃迁的选定规则: 电子每次只能跳跃一级。
13 Raman效应和Raman Transition
Raman Transition也是一种由电子跃迁引起的状态的变化 (Raman不是拉面，是一个印度人名)。简单来说是这么回事：当光子射入液体或者气体中的分子的时候，分子中的电子会吸收光子，处于激发态后，应自发散射出和原光子频率一样的光子，散射方向是随机的。这和之前说的自发emission一致，最终电子的能量不变。这样的散射称为瑞利散射。但是实际上人们发现有1%的散射的光子和原光子的频率不同，这样的散射称为Raman散射。
Raman散射的原理是这样的，当光子被电子吸入后，电子的动能增加，但吸入的能量不足以使得电子跃迁到更高的量子态，而几乎同时，电子自发衰退，射出一个光子，使得电子跃迁到低能量的量子态, 比如上旋变成下旋。
如果我们同时考虑电子的自旋和振动能级，得到如下的量子态
$|\uparrow 0\rangle, |\downarrow 0\rangle, |\uparrow 1\rangle, |\downarrow 1\rangle, |\uparrow 2\rangle, |\downarrow 2\rangle, \dots$
而之前的Raman效应会产生如下的状态转变:
$| \uparrow,n - 1\rangle \rightarrow| \downarrow,n \rangle$
这样的状态转变称为也称为Blue Sideband Transition , (google 上搜不到，只在这篇文章里面提了一下https://phys.auinstallation31.cs.au.dk/fileadmin/site_files/publikationer/phd/Peter_Staanum.pdf Page 24)，如下图所示
Blue Sideband Transition
如果用特定频率的光照射会得到该变换的逆变换，也称为red sideband transition:
$|\downarrow,n \rangle \rightarrow | \uparrow,n - 1\rangle$
Red sideband Transition用于冷却技术。因为经过变换后，离子从基态变为激发态，动能减少，这样当激发态自发衰退到基态后，又可以重复利用这个变换进一步减少动能。如下图所示，其中g表示ground state基态，e 表示excited state激发态
Resolved-sideband cooling using Red Sideband Transition
综上，Blue/Red Sideband Transition合起来称为Raman Transition，(Raman Transition还包括carrier transition，这种变换不改变基态或者激发态。 Raman Transition如下图所示，可以理解为通过动能换取旋转方向的转变。
Raman Transition 包含了 Blue/Red Sideband Transition
14 CNOT Gate的物理实现
现在我们可以实现CNOT Gate了。首先我们将两个钙离子放入由库仑力做成的弹簧中。第一个离子作为控制位。CNOT Gate的规则是如果第一个离子是下旋(0状态)，二号离子不变；否则自旋方向反转。整个操作分3步
假设一号离子的叠加态为 $\alpha | \downarrow 0 \rangle + \beta | \uparrow 0 \rangle$ ，我们用特定的激光照射它，让它产生Raman Transition. 因为 $| \downarrow 0 \rangle$ 不可能Red sideband transition 变为 $| \uparrow -1 \rangle$ , 而 $\beta | \uparrow 0 \rangle$ 被Blue sideband transition成 $\beta | \downarrow 1 \rangle$ 。最终我们得到状态 $\alpha | \downarrow 0 \rangle + \beta | \downarrow 1 \rangle$ 。这样，如果第一个离子原本的上旋转成了动能。如果第一个离子原本是下旋的，则什么都没有发生。
第一个离子上旋产生的动能通过弹簧传递到第二个离子，这样第二个离子的状态就是 $\delta|\downarrow 1\rangle + \gamma|\uparrow 1 \rangle$ ，通过Raman变换， $\delta |\downarrow 1\rangle$ 被Red Sideband Transition成 $\delta |\uparrow 0 \rangle$ ,而 $\gamma \uparrow 1 \rangle$ 被Blue Sideband Transition成 $\gamma \downarrow 2 \rangle$ 。最终得到 $\delta|\uparrow 0 \rangle + \gamma|\downarrow 2 \rangle$ ，这样第二个离子的自旋反转了。
最后我们要恢复第一个离子的状态，我们用与第一步一样的激光再次照射第一个离子，这样 $| \downarrow 1 \rangle$ 被Red Sideband Transition成 $\beta | \uparrow 0 \rangle$ 。最终我们得到到状态 $\alpha | \downarrow 0 \rangle + \beta | \uparrow 0 \rangle$
由于CNOT GATE能拼出任意需要的逻辑门，这样我们也算是理解量子计算机的制作原理了。
15 测量
下图给出了整个量子计算的过程，其中前面的7.5ms用于冷却，制备0状态的量子比特，然后Coherent Manipulation的0.5ms是基于CNOT Gate的逻辑运算，最后的10ms用于测量(Read Out)。
离子阱计算机的计算过程
当电路部分执行完毕，计算机用激光或者微波来维持住自旋的方向。然后我们用另一束经过计算的频率的激光照射这些离子，然后用电荷耦合摄像机 (CCD Camera)观察这些离子。如果离子处于下旋，则相应的位置暗，否则会比较亮。如下图所示。
读取计算结果: 亮的地方表示1，暗的地方表示0
16 与其他物理实现的比较
离子阱算是量子计算机实现的新贵，目前主要是创业公司比如ionQ在研究，还有其他的制作方法，比如超导，核磁共振等等。下图比较了这些实现的优点缺点，离子阱是其中的第二个。离子阱的优点是比较稳定，因为hyperfine structure十分稳定，从而降低出错率。但缺点是每个Gate计算慢，而且需要很多特定频率的激光，和一个极其真空的空间。相比较而言，Google, IBM采用的老牌超导技术，计算十分快速，但是需要一个“冰箱”维持提供几乎绝对零度。现在还没有哪个技术在竞争中处于绝对优势。
不同的量子计算物理实现的比较 https://www.sciencemag.org/news/2016/12/scientists-are-close-building-quantum-computer-can-beat-conventional-one
17 Grover算法
让我们看一个具体的栗子来理解一下量子计算机的优越性吧。这里要讲的Grover算法是要解决这样的问题：
问题: 在 $N = 2^n$ 个数中找某个特定的数 $w$
下面以 $n=3$ 为例子，假设N个数为 $[6,2,3,5,1,0,7,4]$ ，我们要找的数字是 $w = 3$
普通计算机最坏情况 $O(N)$ ，Grover算法 $O(\sqrt{N})$
Grover算法步骤如下：
对 $N$ 个所有数字采用二进制编码, 比如 $3 \rightarrow 011$ ，我们可以用三个比特表示所有的数了。
2. 等概率初始化。之前我们提到通过冷却技术，我们可以得到3个始终为0状态的量子比特。而通过Hadamard门，每个量子比特有1/2概率为0，1/2概率为1. 由于独立性，它们的联合概率分布是均匀的： $|s\rangle = |\psi_0\rangle = \frac{|000\rangle + |001\rangle + \dots + |111\rangle }{\sqrt8}$ ，其中每个编码的系数 $1/\sqrt8$ 称为amplitude
Grover算法初始化, 左边初始化为红色向量，右边amplitude的高度绝对值平方为测量结果为该编码的概率，这里只显示了4个，省略了另4个。红色虚线表示了平均的amplitude大小
3. 制备Oracle门。所谓Oracle门是这么个门 ,其中 $f(x)=\left\{\begin{array} & 1 & 如果x=011 \\ 0 & x\ne 011\end{array}\right.$
当三个比特通过oracle门后，会有
$\mathrm{OracleGate(}|s\rangle) = \frac{|000\rangle + \dots - |011\rangle + \dots }{\sqrt8}$
其实Oracle门所做的是一个镜像变换（其实就是householder变换)。考虑向量 $|w\rangle$ 和 $|\psi_0\rangle$ 构成的平面，Oracle门事实上求得了向量 $|\psi_0\rangle$ 关于与 $|w\rangle$ 垂直直线 $|s'\rangle$ 的对称向量如下图左边所示。这里我们把关于向量 $|z\rangle$ 的镜像变换的变换矩阵记为，因此Oracle门等于 $U_{s'}|s\rangle$ 。而右图中，红色bar反转，表示该分量取反，这样平均的amplitude（红色虚线）下降。
经过Oracle门后，向量作镜像反转，得到红色的向量。右边对应的红色向量的amplification
4 接着关于原向量继续镜像： $U_sU_{s'}|s\rangle$ ，其结果如下图所示，其中红线是之前红线关于向量s的镜像。从右边图看到，红色的bar 的amplitude继续变大，而其他bar的amplitude缩小了。
关于s作镜像。其中编码011的概率继续变大，而其他编码的概率缩小
重复步骤3，4 $\sqrt{N}$ 次之后，011的概率将足够大，测量结果将稳定输出011
关于这个算法的实现可以参考论文 https://arxiv.org/pdf/1703.10535.pdf，如下图所示。整个电路分3快：Init初始化，Oracle实现了步骤3的oracle门，Amplification实现了步骤4。除了初始化运行一次，其他的两个需要重复 $\sqrt{N}$ 次。
Grover算法的逻辑电路 H=Hadamard Gate, Z= Z Gate, X=NOT Gate ，具体参考 https://en.wikipedia.org/wiki/Quantum_logic_gate 或者 https://zhuanlan.zhihu.com/p/21367507
电路用了4个量子比特，最后一个作为辅助。其中H表示Hadamard门，X是逻辑反 $X=\left[\begin{array} & 0 & 1\\ 1 & 0 \end{array}\right]$ ，虚线就是oracle门其中的黑点表示该横线上的量子比特是控制比特，而最后一个 $\oplus$ 表示该横线上的量子比特是被控制的量子比特，当黑点上的量子比特都是1状态时，被控的量子比特反转。虚线右侧是步骤4的实现。Z代表controlled-Z gate: $Z=\left[\begin{array} & 1 & 0\\ 0 & -1 \end{array}\right]$ 。两个黑点加一个Z，就是说如果前两个取1，则第三个经过Z门，否则不变。所有的这些Gate都可以通过CNOT GATE实现。
其实我们可以简单地验证一下。初始状态为 $|0001\rangle$ ，经过4个H门之后，前三个变成 $\frac{|0\rangle + |1\rangle}{2}$ ，最后一个变成 $\frac{|0\rangle - |1\rangle}{2}$ ，因此组合起来是
$\frac{|0000\rangle + |0010\rangle + |0100\rangle + |0110\rangle + |1000\rangle + |1010\rangle + |1100\rangle + |1110\rangle - |0001\rangle - |0011\rangle - |0101\rangle - |0111\rangle - |1001\rangle - |1011\rangle - |1101\rangle - |1111\rangle}{\sqrt{16}}$ 然后是Oracle Gate。第一个比特取反后变成 $\frac{|1000\rangle + |1010\rangle + |1100\rangle + |1110\rangle + |0000\rangle + |0010\rangle + |0100\rangle + |0110\rangle - |1001\rangle - |1011\rangle - |1101\rangle - |1111\rangle - |0001\rangle - |0011\rangle - |0101\rangle - |0111\rangle}{\sqrt{16}}$ 经过那3个黑点和 $\oplus$ 之后，变成 $\frac{|1000\rangle + |1010\rangle + |1100\rangle + |1111\rangle + |0000\rangle + |0010\rangle + |0100\rangle + |0110\rangle - |1001\rangle - |1011\rangle - |1101\rangle - |1110\rangle - |0001\rangle - |0011\rangle - |0101\rangle - |0111\rangle}{\sqrt{16}}$ 然后第一个反转接下来经过4个H门，注意到最后一个辅助比特必须为1，这要求我们必须对最后一位采用 $H\frac{|0\rangle - |1\rangle }{\sqrt2} = |1\rangle$ 的形式，保证产生的都是1。我们先对上面的式子重新排序
$\frac{|0000\rangle - |0001\rangle + |0010\rangle - |0011\rangle + |0100\rangle - |0101\rangle + |0111\rangle - |0110\rangle + |1000\rangle - |1001\rangle + |1010\rangle - |1011\rangle + |1100\rangle - |1101\rangle + |1110\rangle - |1111\rangle}{\sqrt{16}}$ 然后每相邻的两项一组，先让最后一位量子比特左乘H，利用 $H\frac{|0\rangle - |1\rangle }{\sqrt2} = |1\rangle, H\frac{|0\rangle + |1\rangle }{\sqrt2} = |0\rangle$ 得到: $\frac{ |0001\rangle + |0011\rangle + |0101\rangle - |0111\rangle + |1001\rangle + |1011\rangle + |1101\rangle + |1111\rangle}{\sqrt{8}}$
现在最后一位都是1，可以忽略了，得到
$\frac{ |000\rangle + |001\rangle + |010\rangle - |011\rangle + |100\rangle + |101\rangle + |110\rangle + |111\rangle}{\sqrt{8}}$
可以看到， $011$ 的符号变负了，这就是第3步的镜像变换操作。然后三个比特经过H门。先让第三位经过H门，每两个一组，得到
$\frac{ |000\rangle + |011\rangle + |100\rangle + |110\rangle }{\sqrt{4}}$
然后让第二个量子比特过H
$\frac{ |000\rangle + |010\rangle + |001\rangle - |011\rangle}{\sqrt8} + \frac{ |100\rangle }{\sqrt{2}}$
最后让第一个量子比特过H
$\frac{ |000\rangle+ |100\rangle + |010\rangle + |110\rangle + |001\rangle + |101\rangle - |011\rangle - |111\rangle}{\sqrt{16}} + \frac{ |000\rangle - |100\rangle }{\sqrt{4}}$
经过XXX
$\frac{ |111\rangle+ |011\rangle + |101\rangle + |001\rangle + |110\rangle + |010\rangle - |100\rangle - |000\rangle}{\sqrt{16}} + \frac{ |111\rangle - |011\rangle }{\sqrt{4}}$
经过俩黑点的Z门：
$\frac{ -|111\rangle+ |011\rangle + |101\rangle + |001\rangle + |110\rangle + |010\rangle - |100\rangle - |000\rangle}{\sqrt{16}} + \frac{ -|111\rangle - |011\rangle }{\sqrt{4}}$
经过XXX
$\frac{ -|000\rangle+ |100\rangle + |010\rangle + |110\rangle + |001\rangle + |101\rangle - |011\rangle - |111\rangle}{\sqrt{16}} + \frac{ -|000\rangle - |100\rangle }{\sqrt{4}}$
下面经过3个H门，先让第一个量子比特过
$\frac{ - |100\rangle + |010\rangle + |001\rangle - |011\rangle }{\sqrt{8}} + \frac{ -|000\rangle }{\sqrt{2}}$
让第二个量子比特过
$\frac{ - |100\rangle - |110\rangle + |000\rangle - |010\rangle }{\sqrt{16}} + \frac{ |011\rangle -|000\rangle - |010\rangle }{\sqrt{4}}$
让第三个量子比特过
$\begin{array}& &\frac{ - |100\rangle - |101\rangle - |110\rangle - |111\rangle + |000\rangle + |001\rangle - |010\rangle - |011\rangle }{\sqrt{32}} + \frac{ |010\rangle - |011\rangle -|000\rangle - |001\rangle - |010 \rangle - |011\rangle }{\sqrt{8}} \\ =& - \frac{ |100\rangle + |101\rangle + |110\rangle + |111\rangle + |000\rangle + |001\rangle + |010\rangle }{\sqrt{32}} - 5\frac{|011\rangle }{\sqrt{32}} \end{array}$
看，011的概率变大了 !
参考文献
最后给出本文的参考文献，有些文献的内容本文没有涉及，但个人觉得也很有用：
离子阱制作量子计算机 https://medium.com/@jonathan_hui/qc-how-to-build-a-quantum-computer-with-trapped-ions-88b958b81484
超导体制作量子计算机 https://medium.com/@jonathan_hui/qc-how-to-build-a-quantum-computer-with-superconducting-circuit-4c30b1b296cd
Raman Transition https://www2.physics.ox.ac.uk/sites/default/files/JHomethesis.pdf
Paul Trapping https://www.youtube.com/watch?v=u_OlVz95_tw
离子弹簧 https://quantumoptics.at/images/publications/dissertation/hcn_diss.pdf
Yb+ 离子Hyperfine Structure https://www.youtube.com/watch?v=aOm50nPd5kQ&t=
量子数 (quantum number) https://chemed.chem.purdue.edu/genchem/topicreview/bp/ch6/quantum.php
Grover算法的电路 https://arxiv.org/pdf/1703.10535.pdf
Toffoli Gate 电路 https://arxiv.org/pdf/1804.03719.pdf
Grover算法 https://community.qiskit.org/textbook/ch-algorithms/grover.html
CNOT GATE组合成其他Gate: https://zhuanlan.zhihu.com/p/21367507
通用量子门，如何通过CNOT Gate实现任意的幺正变换 https://zhuanlan.zhihu.com/p/72750913
MIT 量子力学公开课 https://www.youtube.com/watch?v=lZ3bPUKo5zc&list=PLUl4u3cNGP61-9PEhRognw5vryrSEVLPr
单摆传递动能实验 https://www.youtube.com/watch?v=v1_-LsQLwkA
施特恩－格拉赫实验 https://www.youtube.com/watch?v=cd2Ua9dKEl8
电子轨道的形状和方向 https://www.youtube.com/watch?v=BzHFBBD-hb4
谐振子模型 https://www.youtube.com/watch?v=Thy9YXnAY2s
振动量子数https://www.youtube.com/watch?v=MUcwscw2mRQ
选定规则 https://www.youtube.com/watch?v=hWo2b-i6UiE
raman effect https://www.youtube.com/watch?v=SsIYDEma_cU
离子阱 PPT http://iontrap.umd.edu/wp-content/uploads/2016/06/ArgonneBenioffFestMay2016.pptx
hadamard gate详细介绍 https://plus.maths.org/content/really-how-do-quantum-computers-work
https://www.zhihu.com/question/30545465/answer/917365011

Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=472

©2021 上海优钧机械设备科技有限公司

Best Last Month

Deep Learning and Reward Design for Reinforcement Learning

Deep Learning and Reward Design for Reinforcement Learning
Information industry

by wittx

Barra模型讲解

Barra模型讲解
Information industry

by wittx

2020/09/29 金融行情

2020/09/29 金融行情
Information industry

by wittx

全球公司融资迎来十年来新高

全球公司融资迎来十年来新高
Information industry

by wittx

基于叙事事理图谱和可扩展图神经⽹络的脚本事件预测模型

基于叙事事理图谱和可扩展图神经⽹络的脚本事件预测模型
Information industry

by wittx

China Launches National Blockchain Network in 100 Cities

China Launches National Blockchain Network in 100 Cities
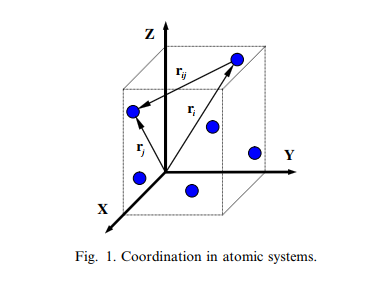
Information industry

by wittx

DeepLearning之优化方法

DeepLearning之优化方法
Information industry

by wittx

二次疫情冲击欧洲经济：商业活动重返萎缩服务业 PMI 创 5 个月新低

二次疫情冲击欧洲经济：商业活动重返萎缩服务业 PMI 创 5 个月新低
Information industry

by wittx

ChatGPT Transformer

ChatGPT Transformer
Information industry

by wittx

恒指午后升幅急速扩大 5 分钟暴力拉涨 300 点

恒指午后升幅急速扩大 5 分钟暴力拉涨 300 点
Information industry

by wittx