
- Investment
- 科学论坛
-
Program
- Recruitment
- Center
News Message
量子计算入门(一):Transmon qubit
- by wittx 2020-10-06
0. 背景
量子计算机实现的最大困难,在于它的物理架构。我们需要一个可以方便制备、操作和测量的两能级量子单元集成系统。理论上,这样的系统有很多,比如:基于液态核磁共振技术的原子核spin qubit,基于非线性Kerr介质的photon qubit,离子阱系统(离子本身当做量子比特),基于半导体量子点的单电子spin qubit,以及基于超导微电路的superconducting qubit,这些比较热门(或者说曾经比较热门)。本栏目主要以超导线路量子系统(superconducting qubit)作为讨论对象,因为它的实验表现远胜于其他几种系统。(真实原因是这个系统最热,所以我只研究了这一个。)
超导量子比特按耦合的对象可以分为不同类别,它们都有不同的电路结构。近年来广受研究讨论的主要是transmon qubit,它在2007年前后由Yale的Robert J. Schoelkopf团队开发完成[1],Google自诩的“量子霸权“就是在基于这个体系的量子计算机上实现的。Schoelkopf的团队几经扩展,现在已经是Yale的一个独立研究所了(Yale Quantum Institute),领衔超导线路量子系统的研究。
Transmon qubit 的全称是“transmission line shunted plasma oscillation qubit”[2],这种设计能够有效压制电荷噪音(charge noise),并且易于制备、集成和扩展。本文作为入门的入门,将从最简单的物理开始讲起。
1. 经典LC振荡电路(LC oscillator)的量子化[3]
这是一个简化的LC振荡电路,由于是超导线路所以没有电阻 记
![[公式]](/images/download/1601955751024_91930.png) 为磁通量(flux),
为磁通量(flux),![[公式]](/images/download/1601955751544_78071.png) 电感常数(inductance),
电感常数(inductance),![[公式]](/images/download/1601955751580_25527.png) 电容常数(capacitance),
电容常数(capacitance),![[公式]](/images/download/1601955751613_22222.png)
![[公式]](/images/download/1601955751644_50199.png) 分别为电压、电流,
分别为电压、电流, ![[公式]](/images/download/1601955751679_85503.png) 为能量。按照电动力学的基本原理:
为能量。按照电动力学的基本原理:![[公式]](/images/download/1601955751725_16475.png)
![[公式]](/images/download/1601955751789_54059.png)
![[公式]](/images/download/1601955751862_96772.png)
![[公式]](/images/download/1601955751911_44252.png)
可得LC振荡电路的拉格朗日量:
![[公式]](/images/download/1601955751965_19309.png)
其中
![[公式]](/images/download/1601955752031_68279.png) 为动能项,
为动能项, ![[公式]](/images/download/1601955752066_55409.png) 为势能项。考虑到电容器上的电荷应满足关系式:
为势能项。考虑到电容器上的电荷应满足关系式:![[公式]](/images/download/1601955752097_41817.png)
我们可以很轻松地得到系统的哈密顿量:
![[公式]](/images/download/1601955752148_80854.png)
这是在经典情境下的经典哈密顿量,小学二年级都会。接下来我们把它一次量子化。我们选择磁通与电荷为一组共轭量,记为算符,满足:
![[公式]](/images/download/1601955752209_49909.png)
方便起见,表示算符的上标将省略。考虑到电感
![[公式]](/images/download/1601955752297_51220.png) 与电容
与电容 ![[公式]](/images/download/1601955752340_12883.png) 都是线性元件,方便起见对磁通和电荷作线性变换,定义约化磁通量和约化电荷数:
都是线性元件,方便起见对磁通和电荷作线性变换,定义约化磁通量和约化电荷数:![[公式]](/images/download/1601955752383_51620.png)
![[公式]](/images/download/1601955752421_68774.png)
![[公式]](/images/download/1601955752456_72327.png) ,为一组正则共轭量。
,为一组正则共轭量。其中
![[公式]](/images/download/1601955752509_70150.png) 为超导磁通量子
为超导磁通量子 ![[公式]](/images/download/1601955752548_34876.png) ,
, ![[公式]](/images/download/1601955752590_57936.png) 实际上就是一对库伯对(Cooper pair)的电量(这已经是一次量子化的体现了),
实际上就是一对库伯对(Cooper pair)的电量(这已经是一次量子化的体现了), ![[公式]](/images/download/1601955752622_45445.png) 的物理意义是电路中增加的库伯电子对数量,
的物理意义是电路中增加的库伯电子对数量, ![[公式]](/images/download/1601955752649_60638.png) 的物理意义是通过规范不变性定义的超导电子的相位(gauge-invariant phase)。接着,记
的物理意义是通过规范不变性定义的超导电子的相位(gauge-invariant phase)。接着,记 ![[公式]](/images/download/1601955752678_48124.png) 为电容上每增加一个电子所带来的能量,
为电容上每增加一个电子所带来的能量, ![[公式]](/images/download/1601955752716_16115.png) 是电感的能量,我们可以写出量子LC振荡电路的哈密顿量:
是电感的能量,我们可以写出量子LC振荡电路的哈密顿量:![[公式]](/images/download/1601955752777_74681.png)
同样地,第一项可以视为动能项,第二项为势能项,从这个角度讲,
![[公式]](/images/download/1601955752828_52995.png) 又充当了广义坐标的角色,较之于量子谐振子(QHO)的哈密顿量:
又充当了广义坐标的角色,较之于量子谐振子(QHO)的哈密顿量:![[公式]](/images/download/1601955752865_67221.png)
显然,真正影响本征解的是势能项,在后文中,我们将对势能项作一些处理。在上式中
![[公式]](/images/download/1601955752915_56989.png) ,使得系统能级结构如下图所示:
,使得系统能级结构如下图所示:它有无穷多个能级,且能级之间的间隔相等,即:
![[公式]](/images/download/1601955753166_72385.png)
![[公式]](/images/download/1601955753207_66018.png) 为系统的共振频率。我们根据QHO的经验对它二次量子化:
为系统的共振频率。我们根据QHO的经验对它二次量子化:![[公式]](/images/download/1601955753256_53207.png)
正则共轭量也同样变换为:
![[公式]](/images/download/1601955753303_27762.png) ,
, ![[公式]](/images/download/1601955753378_20861.png)
![[公式]](/images/download/1601955753457_89898.png) ,
, ![[公式]](/images/download/1601955753501_53163.png)
其中下标 zpf 表示“zero-point fluctuation”,即基态下的量子涨落期望值。
至此,我们得冷静一下,回味一下,为什么我们需要做这些数学变换?本质上讲,上述过程无非是用浅显的量子场论语言把一个经典系统翻译了一遍,意义何在呢?其实从认识论的角度而言,此举并没有什么意义,但从方法论的角度而言,此举将有助于我们这个系统进行改造和操作。须知,沿袭二进制的传统,一个量子比特的运算空间维度只有2. 同时我们对量子比特的调控手段也极其有限,一般是在极短时间内施加特定频率的脉冲来完成门操作(gate operation)。所以,我们必须对上图中包含无数能级的抛物线结构进行“异化”,使它满足两个条件:
- 我们只选用最低的两个能级作为运算空间,记为
![[公式]](/images/download/1601955753560_65347.png) 、
、 ![[公式]](/images/download/1601955753624_82777.png) ,分别代指0、1.
,分别代指0、1. - 能级之间的跃迁频率
![[公式]](/images/download/1601955753654_19857.png) ,
, ![[公式]](/images/download/1601955753685_54164.png) ...... 必须不同,否则计算空间将一片混乱。
...... 必须不同,否则计算空间将一片混乱。
总体而言,这个LC电路越不和谐越好,越非线性越好。为此,我们要用到所有超导线路量子系统共通的核心元件:约瑟夫森结(JJ)。这个非线性、无耗散的电路元件,将会给哈密顿量带来一些变化,之后我们会发现,这个变化,用量子场论的语言更易于描述。
2. 约瑟夫森结(Josephson Junction)和 transmon qubit
JJ的简单构造:两片超导体夹一层绝缘体 根据BCS理论,超导电子可用一个有效波函数来表示
![[公式]](/images/download/1601955753948_86756.png) ,其中
,其中 ![[公式]](/images/download/1601955754003_14905.png) 代表Cooper pair个数,
代表Cooper pair个数, ![[公式]](/images/download/1601955754051_96496.png) 代表波函数相位。如果两个超导体距离很近,则其分布于表面的Cooper pair会相互耦合,其波函数相位会发生联系。由于隧穿效应,Cooper pair就会在两个超导体间进行流动,形成超导电流。在两个超导体之间夹入一层薄薄的绝缘介质,即构成约瑟夫森结。当超导电流流过约瑟夫森结时,结中会储存一定的能量,其行为类似于电感。用约瑟夫森结替代电感接入LC oscillator,如下图所示,就构成了一个transmon qubit,设计非常简单。
代表波函数相位。如果两个超导体距离很近,则其分布于表面的Cooper pair会相互耦合,其波函数相位会发生联系。由于隧穿效应,Cooper pair就会在两个超导体间进行流动,形成超导电流。在两个超导体之间夹入一层薄薄的绝缘介质,即构成约瑟夫森结。当超导电流流过约瑟夫森结时,结中会储存一定的能量,其行为类似于电感。用约瑟夫森结替代电感接入LC oscillator,如下图所示,就构成了一个transmon qubit,设计非常简单。transmon qubit 电路示意图,约瑟夫森结自带电感电容 我们需要计算约瑟夫森结在电路中存储的能量,以得到系统哈密顿量。这里需要用到两个约瑟夫森关系:
![[公式]](/images/download/1601955754317_28016.png)
![[公式]](/images/download/1601955754353_84447.png)
其中
![[公式]](/images/download/1601955754397_89032.png) 为临界电流,是由材料性质决定的常数;它的物理意义是约瑟夫森结在转换到非零电压电阻状态之前,所能承载的最大超导电流。这两组关系的物理意义和推导过程都非常简单,任何一本讲超导物理的教科书都会涉及,我就不抄书了。黄昆在《固体物理学》中引述了费曼的推导方式,只需要基础量子力学便可完成,非常优美,建议一阅。
为临界电流,是由材料性质决定的常数;它的物理意义是约瑟夫森结在转换到非零电压电阻状态之前,所能承载的最大超导电流。这两组关系的物理意义和推导过程都非常简单,任何一本讲超导物理的教科书都会涉及,我就不抄书了。黄昆在《固体物理学》中引述了费曼的推导方式,只需要基础量子力学便可完成,非常优美,建议一阅。根据静电能的定义式,易得:
![[公式]](/images/download/1601955754426_93837.png)
记
![[公式]](/images/download/1601955754518_17426.png) . 由于我们总可以通过选择能标消去常数项,故约瑟夫森结的势能
. 由于我们总可以通过选择能标消去常数项,故约瑟夫森结的势能 ![[公式]](/images/download/1601955754573_19069.png)
![[公式]](/images/download/1601955754606_38581.png) . 整个电路的哈密顿量改写成:
. 整个电路的哈密顿量改写成:![[公式]](/images/download/1601955754665_63995.png)
其中
![[公式]](/images/download/1601955754726_86581.png)
![[公式]](/images/download/1601955754760_87660.png) 是总电容。可见,在电路中引入约瑟夫森结后,势能具有余弦形式,使得能谱不再简并,从而使我们能够识别出唯一可寻址的量子二能级系统。
是总电容。可见,在电路中引入约瑟夫森结后,势能具有余弦形式,使得能谱不再简并,从而使我们能够识别出唯一可寻址的量子二能级系统。约瑟夫森电感将二次函数的能谱(红色虚线)重塑为三角函数(纯蓝色),形成了具有唯一能量差的两个计算基底,0和1. 实际上,根据约瑟夫森结制备材料的性质,
![[公式]](/images/download/1601955755006_24485.png) 和
和 ![[公式]](/images/download/1601955755049_81392.png) 是两个独立的、可预调的变量。系统的动力学由何种能量主导,取决于
是两个独立的、可预调的变量。系统的动力学由何种能量主导,取决于 ![[公式]](/images/download/1601955755122_21179.png) 这个比值。当
这个比值。当 ![[公式]](/images/download/1601955755153_91724.png) 时,量子比特对电荷噪音(charge noise)高度敏感,而电荷噪音非常难以抑制,大大缩短了退相干时长(decoherence time)。所以,我们必须要求:
时,量子比特对电荷噪音(charge noise)高度敏感,而电荷噪音非常难以抑制,大大缩短了退相干时长(decoherence time)。所以,我们必须要求:![[公式]](/images/download/1601955755188_71417.png)
由于
![[公式]](/images/download/1601955755227_20203.png) 的大小取决于
的大小取决于 ![[公式]](/images/download/1601955755268_98532.png) ,其中
,其中 ![[公式]](/images/download/1601955755315_14569.png) 是并联电容,
是并联电容, ![[公式]](/images/download/1601955755349_80716.png) 是JJ自带的电容,所以,为了减小
是JJ自带的电容,所以,为了减小 ![[公式]](/images/download/1601955755397_66310.png) ,我们需要增大
,我们需要增大 ![[公式]](/images/download/1601955755421_48002.png) ——之所以不是
——之所以不是 ![[公式]](/images/download/1601955755459_32859.png) 原因在于技术上
原因在于技术上 ![[公式]](/images/download/1601955755492_86220.png) 更好调。这等效于要求
更好调。这等效于要求 ![[公式]](/images/download/1601955755532_88874.png) ,只有满足这个条件,上图的电路才是一个真正意义上的 transmon qubit. 此时,超导相位
,只有满足这个条件,上图的电路才是一个真正意义上的 transmon qubit. 此时,超导相位 ![[公式]](/images/download/1601955755566_28474.png) 是个好量子数(即守恒量,与哈密顿量对易),并且量子涨落很小。为了更充分地认识这一约化过程,我们可以将势能项
是个好量子数(即守恒量,与哈密顿量对易),并且量子涨落很小。为了更充分地认识这一约化过程,我们可以将势能项 ![[公式]](/images/download/1601955755595_29423.png) 在
在 ![[公式]](/images/download/1601955755634_57976.png) 上展开:
上展开:![[公式]](/images/download/1601955755661_40709.png)
![[公式]](/images/download/1601955755697_38286.png)
该式中第一项就是QHO的势能项,第二项造就了非谐性,调制了本征解。我们可以就此定义非谐系数
![[公式]](/images/download/1601955755752_47834.png) . 对于一般 transmon 设计而言,
. 对于一般 transmon 设计而言, ![[公式]](/images/download/1601955755793_94547.png) ,
,以确保比特自身的频率(qubit frequency)
![[公式]](/images/download/1601955755844_16194.png) ,
,同时让势能项足以压制电荷噪音
![[公式]](/images/download/1601955755908_45969.png) .
.对于展开式
![[公式]](/images/download/1601955755959_69694.png) 如果只考虑到四次项,用量子场论的语言来描述,那么它的形式类似于杜芬振子(Duffing Oscillator)的二次量子化哈密顿量:
如果只考虑到四次项,用量子场论的语言来描述,那么它的形式类似于杜芬振子(Duffing Oscillator)的二次量子化哈密顿量:![[公式]](/images/download/1601955756026_59727.png)
这个式子非常重要,是后续量子比特研究的基础性哈密顿量。在接下来几章中我们会看到,当今前沿的量子比特理论研究,都是在这个哈密顿量上做文章。不过回想一下,这个哈密顿量是什么?实际上它是用量子场论的语言给势能项
![[公式]](/images/download/1601955756083_67634.png) 的近似。考虑到动能项是预先设定的(并联电容
的近似。考虑到动能项是预先设定的(并联电容 ![[公式]](/images/download/1601955756120_86356.png) 是预先设计好刻在氧化铝片上的,请参考下图,电容被做的非常大),所以
是预先设计好刻在氧化铝片上的,请参考下图,电容被做的非常大),所以 ![[公式]](/images/download/1601955756146_24283.png) 只是
只是 ![[公式]](/images/download/1601955756179_78445.png) 的函数,于是把
的函数,于是把 ![[公式]](/images/download/1601955756215_63824.png) 变换为
变换为 ![[公式]](/images/download/1601955756252_27592.png) 的代数式(即用QHO的eigenbases展开),方便后续操作。
的代数式(即用QHO的eigenbases展开),方便后续操作。虽然transmon的电路看起来简单,但加上门电路、读取电路、调制电路之后,整个系统是非常复杂的,况且,这还只是一个transmon qubit. 注:电路设计不是唯一的。 值得一提的是,由于在实验中
![[公式]](/images/download/1601955757060_68831.png) ,并且如果对高能级的激发可以被压制(比如使用更大的
,并且如果对高能级的激发可以被压制(比如使用更大的 ![[公式]](/images/download/1601955757093_60241.png) 或更稳健的量子绝热门),则该哈密顿量可以进一步等效为:
或更稳健的量子绝热门),则该哈密顿量可以进一步等效为:![[公式]](/images/download/1601955757124_79406.png)
其中
![[公式]](/images/download/1601955757166_63699.png) 为泡利z矩阵(Pauli-z operator). 需要指出:如何约化,视具体情境而定。
为泡利z矩阵(Pauli-z operator). 需要指出:如何约化,视具体情境而定。3. 量子比特耦合的哈密顿量
前文中涉及到 Duffing oscillator 这个术语,需要解释一下。它原本描述的是一个受周期力驱动的振子,在分析力学中有较为重要的地位,因为它的波动方程
http://www.cfm.brown.edu/people/dobrush/am34/Mathematica/ch3/duffing.htmlwww.cfm.brown.edu![[公式]](/images/download/1601955757196_47428.png) 没有解析解,通过调节阻尼项
没有解析解,通过调节阻尼项 ![[公式]](/images/download/1601955757278_16357.png) 可以用来研究混沌系统。有趣的是,物理研究者似乎不怎么关心这个东西,仅仅是用了它的名字而已。我在wiki和Scholarpedia上索源,发现研究者主要是数学背景的。所以,从逻辑上来讲,Duffing oscillator对整个Circuit QED 知识体系架构只是贡献了一个名字而已,没有内涵可言。在此分享布朗大学数学系的一个课程网页以供参考。
可以用来研究混沌系统。有趣的是,物理研究者似乎不怎么关心这个东西,仅仅是用了它的名字而已。我在wiki和Scholarpedia上索源,发现研究者主要是数学背景的。所以,从逻辑上来讲,Duffing oscillator对整个Circuit QED 知识体系架构只是贡献了一个名字而已,没有内涵可言。在此分享布朗大学数学系的一个课程网页以供参考。Duffing Oscillator Hamiltonian 的形式,上文已经写过了:
![[公式]](/images/download/1601955757313_70718.png)
它被用以描述一个 transmon qubit 的哈密顿量。众所周知,量子计算肯定是基于耦合的量子系统的,那么对于两个耦合在一起的 transmon qubit,哈密顿量是怎样的呢?
不考虑工程技术问题,理论上两个系统的耦合只需在其简单加和的基础上再加上相互作用项,而相互作用由各自的eigenbases决定,即
![[公式]](/images/download/1601955757363_76671.png)
正如本文一开始所说,超导量子线路的耦合方式有很多种,
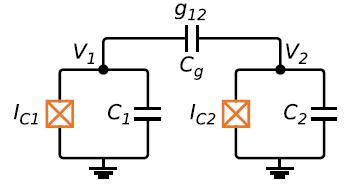
![[公式]](/images/download/1601955757408_72355.png) 的形式不尽相同。对于 transmon qubit 来说,比较简易的耦合方式是通过电容(capacitively coupled),如下图所示
的形式不尽相同。对于 transmon qubit 来说,比较简易的耦合方式是通过电容(capacitively coupled),如下图所示这种耦合方式其实不好。Coupler本质上也是一种gate,现在已经开发出了很多性能优越的gate来实现双量子比特耦合(至少理论上很优越) 此时,
![[公式]](/images/download/1601955757683_45075.png) 可表示为
可表示为 ![[公式]](/images/download/1601955757713_55909.png) ,其中
,其中 ![[公式]](/images/download/1601955757764_94878.png) 是耦合常数。考虑到
是耦合常数。考虑到 ![[公式]](/images/download/1601955757795_90368.png) ,这个简易的双量子比特耦合系统的哈密顿量可以表示为:
,这个简易的双量子比特耦合系统的哈密顿量可以表示为:![[公式]](/images/download/1601955757831_65753.png)
将它二次量子化,得到:
![[公式]](/images/download/1601955757902_71505.png)
式中第一项为两个 Duffing oscillators 的叠加,第二项代入了
![[公式]](/images/download/1601955757985_93252.png) 一式,
一式,![[公式]](/images/download/1601955758025_55692.png) 是耦合常数(为什么要再定义一遍耦合常数?原因在于这些常数从来都不是确定的,你不知道它到底经历了什么,也不需要知道,所以不妨给个新名字,就理论研究而言,这种常数的内部结构并不重要)。如果忽略更高的能级(须知,能级永远可以往上激发,我们不可能真的“抹掉”
是耦合常数(为什么要再定义一遍耦合常数?原因在于这些常数从来都不是确定的,你不知道它到底经历了什么,也不需要知道,所以不妨给个新名字,就理论研究而言,这种常数的内部结构并不重要)。如果忽略更高的能级(须知,能级永远可以往上激发,我们不可能真的“抹掉” ![[公式]](/images/download/1601955758053_28427.png) 的能级),其形式可以简化为:
的能级),其形式可以简化为:![[公式]](/images/download/1601955758083_51599.png)
这个形式的哈密顿量,就是两个自旋量子比特(spin qubit )耦合的哈密顿量。为什么要推导这个形式?因为它在理论研究中也经常用到。一般做理论的人不关心用何种系统去实践量子计算,原则上来讲,系统与系统之间都是等价的,比如我们从 transmon qubit 的哈密顿量出发可以约化到 spin qubit 的哈密顿量。由于一些历史原因,理论研究者似乎对 spin qubit 有种特殊的偏好,大概是因为作为自旋本征态的 up and down 天生对应了 0 和 1,尽管实验上我们几乎不可能把一个个电子摆好去操弄它们的自旋。
参考
- ^Koch, J., Terri, M. Y., Gambetta, J., Houck, A. A., Schuster, D. I., Majer, J., ... & Schoelkopf, R. J. (2007). Charge-insensitive qubit design derived from the Cooper pair box. Physical Review A, 76(4), 042319.
- ^Fink, J. M. (2010). Quantum nonlinearities in strong coupling circuit QED (Doctoral dissertation, ETH Zurich).
- ^Krantz, P., Kjaergaard, M., Yan, F., Orlando, T. P., Gustavsson, S., & Oliver, W. D. (2019). A quantum engineer's guide to superconducting qubits. Applied Physics Reviews, 6(2), 021318.
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=470

Best Last Month
Information industry by wittx
Electronic electrician by wittx

Information industry by wittx
Information industry by show

Information industry by wittx
Information industry by wittx

Information industry by wittx

Information industry by wittx
.jpg)
Mechanical electromechanical by wittx

Information industry by wittx







