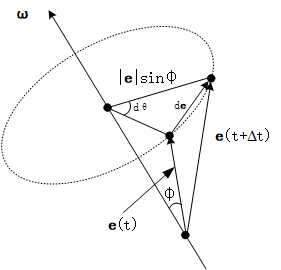
第1小节 拉格朗日方程的由来

在经典力学中我们知道若要知道物体的运动，需要选取牛顿第一定律成立的惯性参考系，然后对物体利用牛顿第二定律列写微分方程组，若要解这个微分方程组，需要添加相应的约束。说白了，就是建立质点系平衡条件。那我们能不能进一步的推导，将约束条件与微分方程放在同一个公式中？建立一个与牛顿体系不同的平衡条件呢？事情的开始是从达朗贝尔原理说起。

质点的达朗贝尔原理：作用在质点上的主动力、约束力与虚加的惯性力在形式上组成平衡力。

质点系的达朗贝尔原理：质点系中每个质点上作用的主动力、约束力与惯性力在形式上组成平衡力系。

说的通俗一点就是将惯性引起的力也要受力分析，但这个力并不是真正意义上的力，只是在形式上可以看作力。

接下来再介绍虚位移原理，介绍之前先解释一下虚位移：在给定位置上质点或质点系在约束所容许的条件下可能发生的任何无限小位移，称为质点或质点系的虚位移。

这个概念中有几处不好理解的地方：

（1）约束所容许的条件：不能破坏系统约束的条件。

（2）可能发生：这个是假象的，与时间无关

（3）无限小：即不改变系统的状态（位置、速度、加速度等其他物理量）。

虚位移原理：具有双面、稳定、理想约束的质点系，在给定位置平衡的必要与充分条件是：所有作用于质点系的主动力在质点的任何虚位移中的虚功之和等于零。对于任意的物理系统，所有惯性力或施加的外力，经过符合约束条件的虚位移，所作的虚功的总合为零。

现假设一粒子  的位置  为广义坐标  的函数，即

所受外力为 ，其虚位移为

带入虚位移原理的公式中

令

则公式1变为

由于

则

因为

因此

又因为

因此

令

则

因此

然后带入公式2中得

因此

这就是基本形式的拉格朗日方程，又叫做第二类拉格朗日方程。

为保证正确，拉格朗日方程我又自己从头到尾推导了一遍，实在太消耗精力了，请各位小伙伴不要急躁，若有错误或不明白的地方，请各位小伙伴们在评论区写出来。

第2小节 拉格朗日方法对机器人进行动力学分析

牛顿方法分析动力学时在分析的过程中可以知道所有连杆生成运动的方向以及大小，虽然这个是优点，但缺点也显而易见，分析太过复杂，若系统复杂，出错的机会就会大大提高；而拉格朗日方法分析动力学是以能量的角度来看待系统的，但两者分析的结果却是相同的。

对于连杆而言，其动能包含连杆质心的动能以及绕质心旋转的动能两部分，即

上面的公式是一个连杆的动能，所有连杆的动能为

这个动能是一个关于角度与角速度的函数，即

Best Last Month

无线电通信

Information industry

by wittx

太阳能电池能量转化率25.4%

Information industry

by wittx

Google Brain的优化器Lion

Information industry

by wittx

Machine learning-eabled constrained multi-objective desig of architected materials

Information industry

by wittx

腾讯音乐三季度营收实现超预期增长

Information industry

by wittx

arxiv Computer Science

Information industry

by wittx

How the gravity engine createed

Information industry

by wittx

Black-Litterman模型介绍

Information industry

by wittx

2020/12/26 金融行情

Information industry

by wittx

石墨烯实现超级电容电池

Electronic electrician

by wittx