机器人运动控制算法3--Intelligent technology investment network-上海优钧机械设备科技

News Message

机器人运动控制算法3

by wittx 2020-06-07

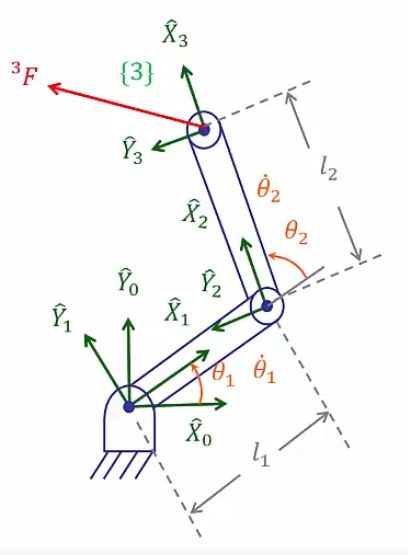
机器人运动控制算法3

第1小节静力分析

由于操作臂的链式结构，力和力矩是从一个连杆向下一个连杆传递的，但是这个传递的机制是怎样的呢？接下来我们来了解一下，为方便理解，我们先从最简单的静力开始思考与理解。

第一部分，对于操作臂的静力操作，使各个连杆固定不动，对各个连杆进行讨论，写出力与力矩对于各连杆坐标系的平衡关系；

第二部分，为保持操作臂的静态平衡，计算所需的各关节轴上所施加的力与力矩。

这一节在分析时忽略重力（以后的章节中再将重力添加进去）。

一个连杆在静止的情况下受力平衡，接下来分析连杆受力

图中 $f_{i}$ 表示在{i}坐标系中的受力， $n_{i}$ 表示在{i}坐标系中的力矩。

现在该连杆受力平衡，因此，

$^{i}f_{i}=^{i}f_{i+1}=_{i+1}^{i}R^{i+1}f_{i+1}$

$^{i}n_{i}=^{i}n_{i+1}+^{i}P_{i+1}\times ^{i}f_{i+1}=_{i+1}^{i}R^{i+1}n_{i+1}+^{i}P_{i+1}\times ^{i}f_{i+1}$

这里和速度推导的公式不太一样，在推导末端速度时，是底座固定不动，按照离底座的距离的方式从近到远进行推导，这里静力的推导式按照从远到近的方式进行推导。为什么要这样推导？？？

因为这里假设的是在机器人末端受力！！！如果是机器人其他地方受力呢？也可以！！！只不过要把这个力或力矩变换到末端去！！！我不变换行不行？也可以，只要在受力分析的时候把力或力矩加到受力的连杆坐标系中！！！但是这样太麻烦了，因为不是所有的机器人控制器底层都对我们开放！！！要额外花钱的！！！

将各个连杆坐标系中的力和力矩向各连杆坐标系的Z轴做投影，就是使机器人保持静止时各轴上的电机所需要输出的力矩。

$\tau_{i}=^{i}n_{i}^{T}{}^{i}Z_{i} 或 \tau_{i}=^{i}f_{i}^{T}{}^{i}Z_{i}$

在机器人设计的时候，在不改变末端载荷的要求下，尽量让各轴上电机承受的力矩要小一些，也就是尽量让结构去承载比较大的力和力矩。

第2小节力雅可比

机器人在静态下，可知关节力矩与作用在末端的力或力矩时平衡的，如果有位移，就会做功，若将位移趋向于无穷小，即可以用虚功原理来描述静止的情况，因为功是能量单位，它在任何广义坐标系中测量的结果是相同的，于是有，

$F\cdot\delta x=\tau\cdot\delta\theta$

第2章内容中的雅可比矩阵定义为，

$\delta x=J\delta\theta$

因此可以写出，

$F^{T}J\delta \theta=\tau^{T}\delta\theta$

即，

$\tau=J^{T}F$

第3小节静力分析例子

这里只举了外力作用在末端，不含外力矩地情况， $^{3}F$ 即外力。已知

静力分析：

因此，

Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=278

©2021 上海优钧机械设备科技有限公司

Best Last Month

Robot Lecture

Robot Lecture
Information industry

by wittx

新东方香港 IPO 募资 10 亿美元

新东方香港 IPO 募资 10 亿美元
Information industry

by wittx

调整数据权重，性能提升6.5%，速度提升2.6倍

调整数据权重，性能提升6.5%，速度提升2.6倍
Information industry

by wittx

并购收购重组

并购收购重组
Information industry

by wittx

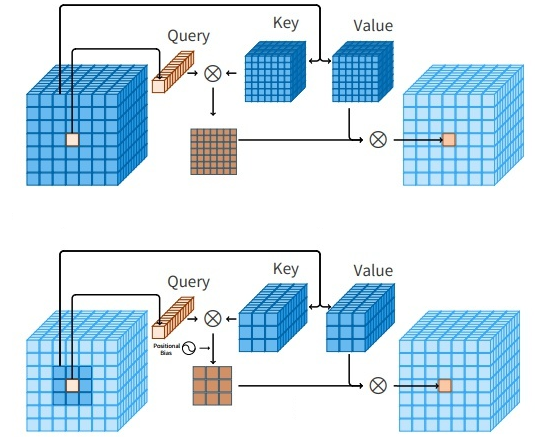
Swin Transformer

Swin Transformer
Information industry

by wittx

Design and Manufacturing of a Miniature Turbojet Engine 航空发动机设计

Design and Manufacturing of a Miniature Turbojet Engine 航空发动机设计
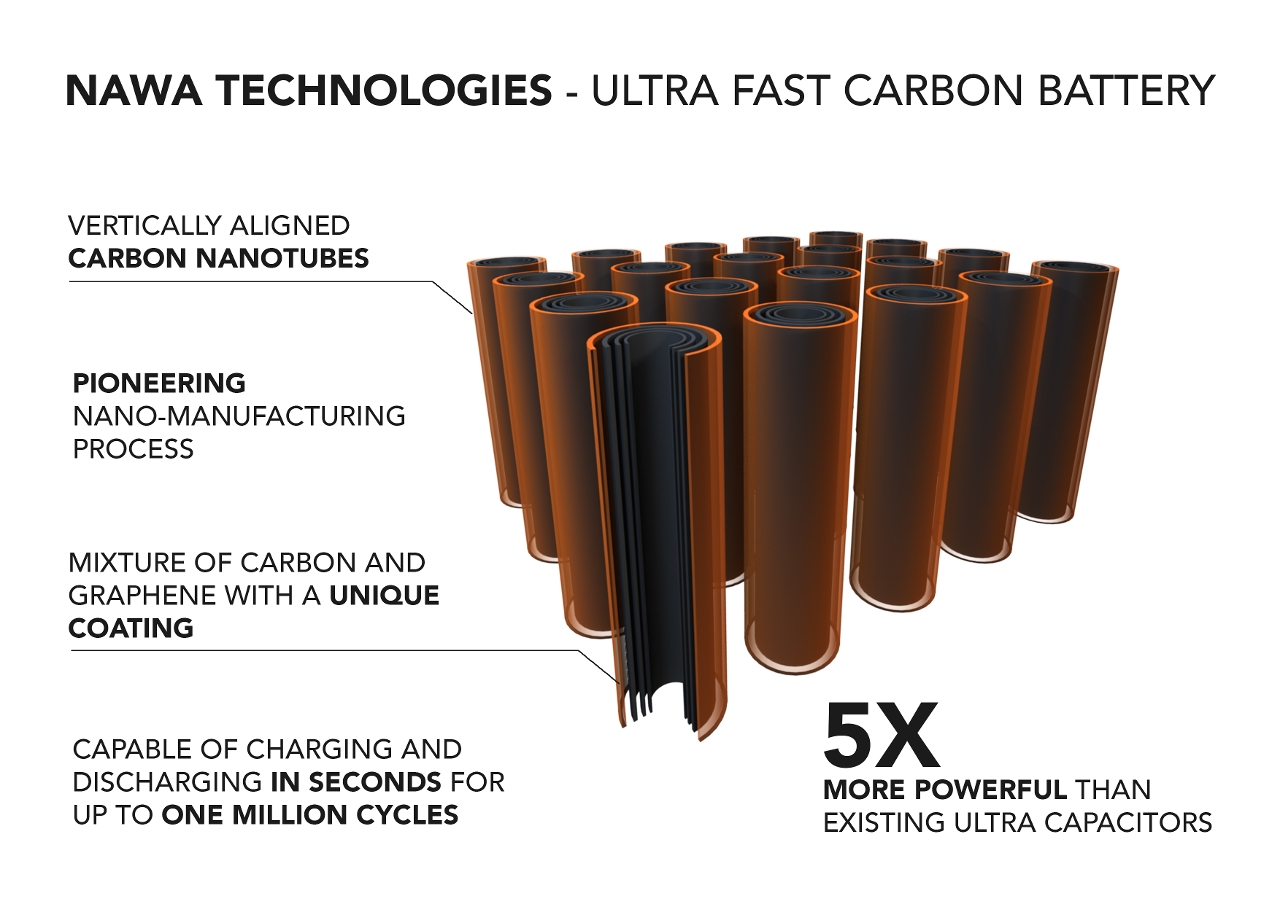
Information industry

by wittx

纳米技术超级电容器提升电动汽车的能量密度

纳米技术超级电容器提升电动汽车的能量密度
Information industry

by wittx

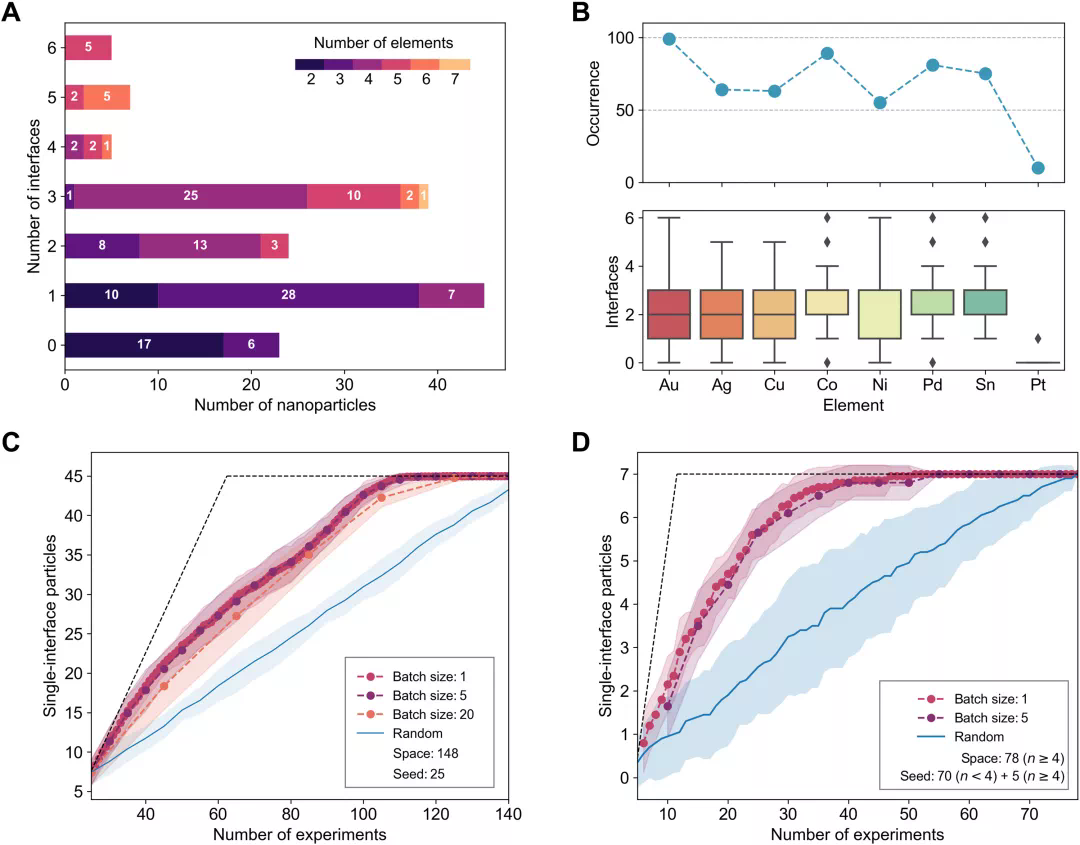
准确率达 95%，机器学习预测复杂新材料合成

准确率达 95%，机器学习预测复杂新材料合成
Information industry

by wittx

硬件设备操作系统

硬件设备操作系统
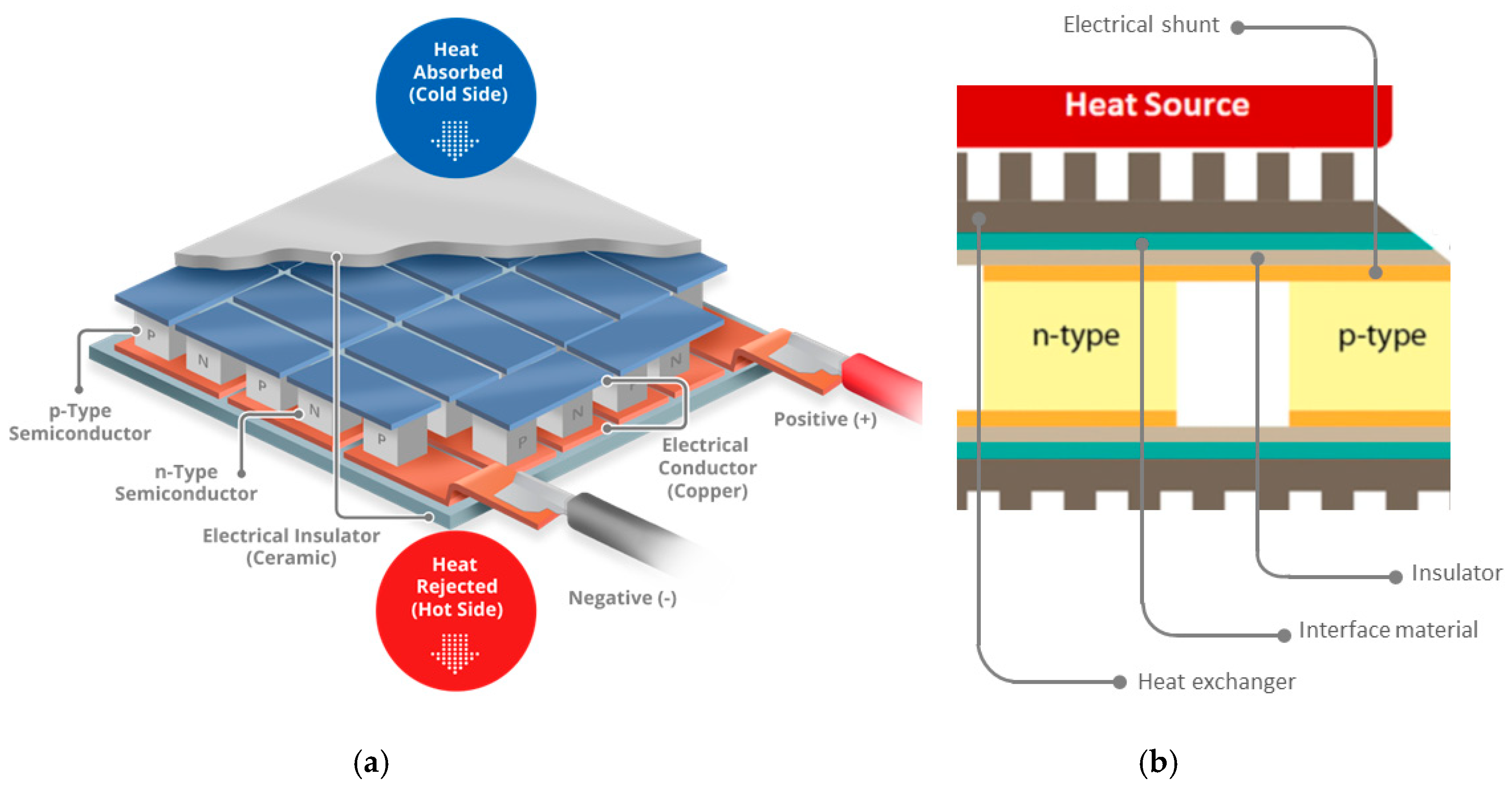
Information industry

by wittx

Three dimensional architected thermoelectric devices with high toughness and power conversion effici

Three dimensional architected thermoelectric devices with high toughness and power conversion effici
Information industry

by wittx