本文根据作者的ACC讲稿FOAD:Fast Optimization Based Autonomous Driving Motion Planner整理而成。FOAD的主要优点有:1)稳定性,保证了存在底层控制器误差的情况下的闭环稳定性;2)实时性,可以至少支持10Hz的实时规划及再规划频率;3)广适性,可以处理多种复杂场景。
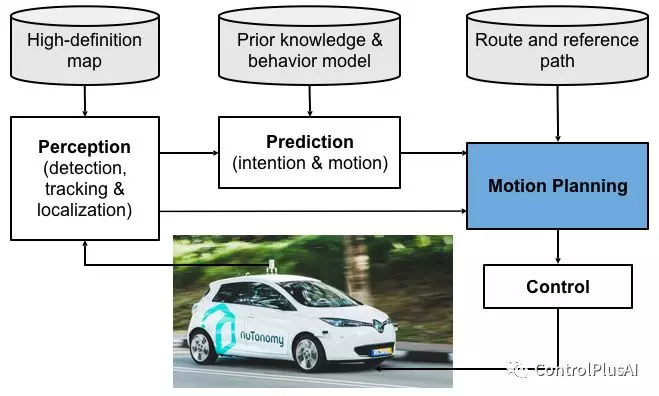
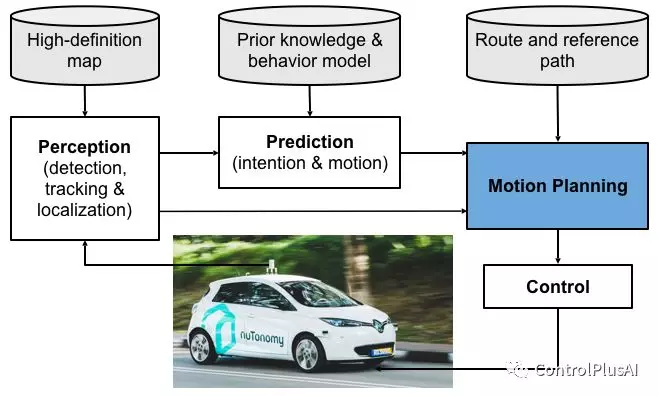
在自动驾驶软件的开发中,运动规划是最核心的模块之一。它将综合来自感知,定位和地图等信息,规划出无人车未来一段时间(约10秒)的一系列动作指令(方向盘转角,油门,刹车等)。为了更加量化地描述这一过程,我们用两个部分来定义一个运动规划的问题——目标函数(objective function)和约束(constraint)。运动规划的最终目的就是找出一条最优的运动轨迹,使其能够最小化(或者最大化)目标函数,并且不违背任何约束。在自动驾驶中,这两部分主要包含了以下内容:
目标函数:
驾驶行为:例如舒适性,能耗和驾驶效率等;
软性交通规则:例如车道保持以及限速等;
约束:
碰撞规避:无人车不能在任何时刻与任何障碍物发生碰撞。障碍物可以是静止的也可以是运动的;
硬性交通规则:例如红绿灯指示,停车线等;
车辆动力学:所规划的轨迹需要满足车身动力学方程,以及方向盘转角限制,加速度限制等。
机器人学家们提出了多种方案来解决运动规划问题,它们按照主要思想可以大致分为搜索法(search-based),采样法(sampling-based) 以及数值优化法(optimization-based)等。目前并没有说哪一种方法就一定是最好的,它们各有所长,主要还是看应用场景。由于这是一门内容相当丰富的学科,我们在此无法详细介绍,感兴趣的同学可以参考参考相关书籍《Principles of Robot Motion》,《PlanningAlgorithms》,本文将主要介绍我们设计的一种基于数值优化的规划算法。之所以选择使用数值优化法,是因为看中了它相比于其他方法的一些优势:
(1) 准确性:基于优化算法的规划在连续空间中进行,不需要离散化;
(2) 完备性:无论可行区域多么狭小都能找到解,不像搜索法等,它们要求分辨率足够小,而过于精细的分辨率会使得计算量爆炸式增长;
(3) 高效性:在优化中整条轨迹可以同时进行调整,而不是像搜索或采样法那样需要按照时间顺序展开。
但是在无人车的应用场景中,优化算法同时也面临着很多挑战,它们主要来自两个方面:
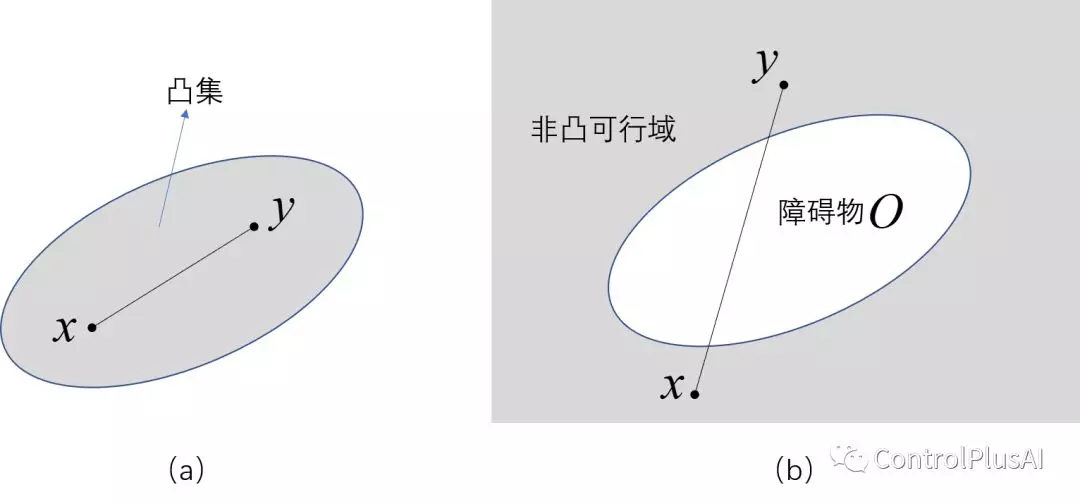
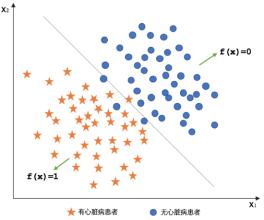
(1) 非凸可行域(non-convex feasible set):我们首先简单介绍一下凸集(convex set)的概念。如图一(a)中所示,在一个凸集中,任意取两点x和y,其连线段上的任意一点任然属于这个集合。若一个集合无法满足上述条件则它就是非凸的。如图一(b)所示,假设O集合代表了一个障碍物,其包含的区域我们不能进入,这就使得我们的可行域变成了非凸的。而对无人车来说,有可能到处都是障碍物,这使得整个可行域呈现高度非凸性。由于优化中的大多数工具都依赖凸的性质,因此这种高度非凸性给数值优化带来了很大的困难。
图一:(a)椭圆表示一个凸集,其中任意两点x,y的连线段上的点都在此集中。(b)椭圆表示障碍物,障碍物之外的区域为可行域,由于此可行域集合不是凸的,因此它是一个非凸可行域。
(2) 高维度(high dimensionality):虽然我们用来描述一辆车的当前状态的维度并不高,比如其位置x,y一共二维。然而当我们把整条轨迹上的状态叠起来时,就会形成一个高维度的向量[x1,y1,...,xN,yN]。这里下标表示时间戳,在我们的应用中N大概是40~50步,这样整个向量的维度就达到接近一百维。而我们的优化正是以这个高维向量作为决策变量的。
上述挑战使得用优化方法来解自动驾驶运动规划变得十分困难,而自动驾驶又对实时性要求极高。事实上现在在自动驾驶上的数值优化规划算法的应用都做了较大的妥协,要么是减少了所考虑的轨迹长度,使得无人车变得短视,要么是进行了大量的线性化,使得最终结果不够精确。
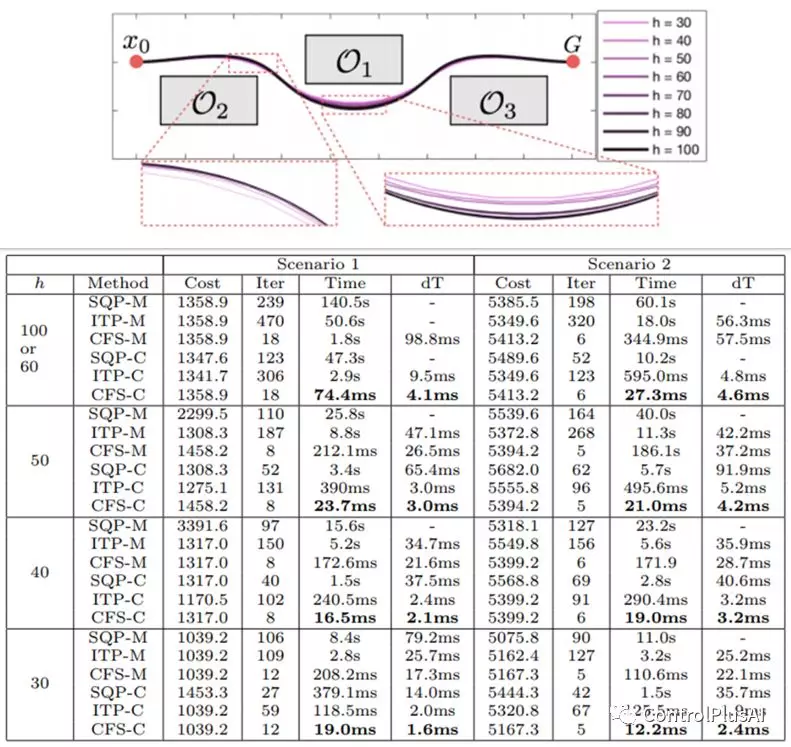
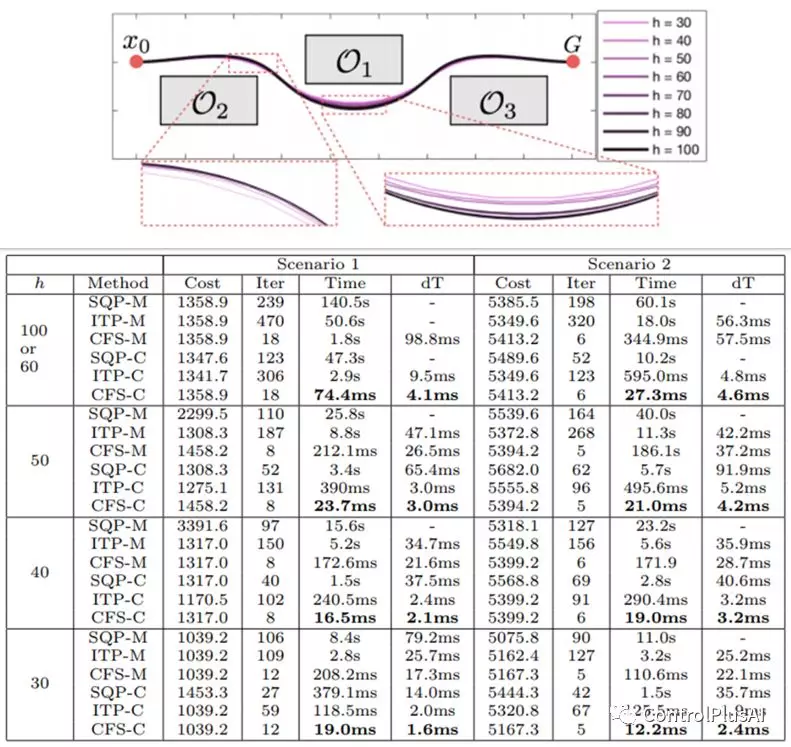
我们提出了一种名为凸可行集的优化算法[1],在一系列仿真场景测试中,我们发现它不仅能非常稳定地在错综复杂的障碍物中找出一条最优轨迹,而且其效率远高于现有的算法(如图二)。
图二:凸可行集算法(CFS)与序列二次规划(SQP)和内点法(ITP)在Matlab(XXX-M)和C++(XXX-C)上的计算效率比较。
将CFS算法应用于一个车辆模型后,得力于其快速性和处理非凸优化问题的有效性,无人车能够在极复杂的环境中快速找到一条到达目标地点的最优运动轨迹(如图三)。
图三:蓝色方块为无人车,黄色方块为障碍车,红色虚线框为无人车需要到达的目标地点。
然而以上只是开环地规划了一条从起点到终点的轨迹,在无人车的应用中,为了应对不断变化的环境,我们必须根据新接收到的环境感知数据不断地重新规划。这时在每次重规划时直接使用CFS算法将使得系统变得不稳定,原因是底层轨迹跟踪控制无法完美跟踪规划出来的轨迹,导致下一时刻的系统约束可能受到违背。为了应对此问题,我们提出了软约束凸可行集(SCCFS)算法。我们在约束边界附近加了一片缓冲区,在这个缓冲区内制造了一定的排斥势场,使得约束条件更加鲁棒。最终我们成功地将算法应用在了无人车的运动规划中[2],下面展示一些应用结果。首先是一个双车道多车超车场景仿真:
图四:双车道超车场景。其中蓝色方框代表无人车,红色方框代表其他车辆,红色点画线代表所规划的轨迹。
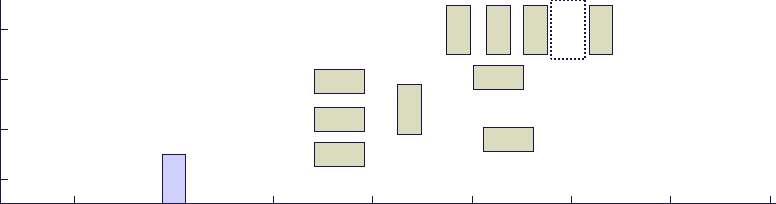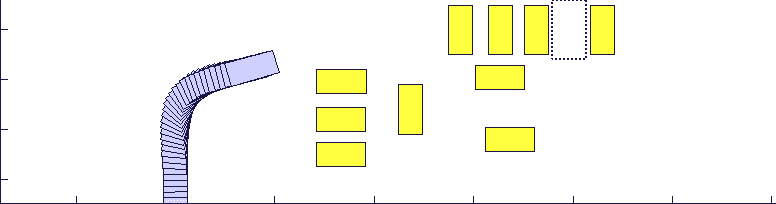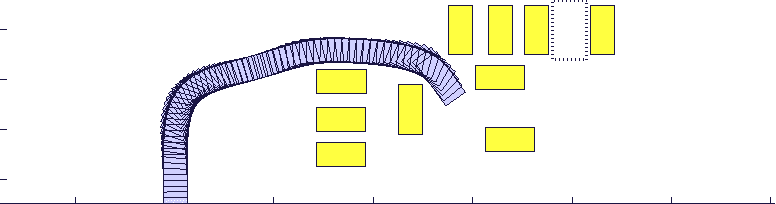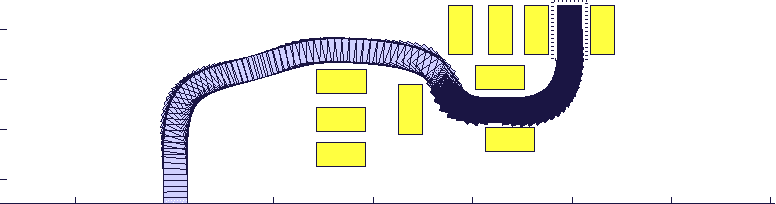
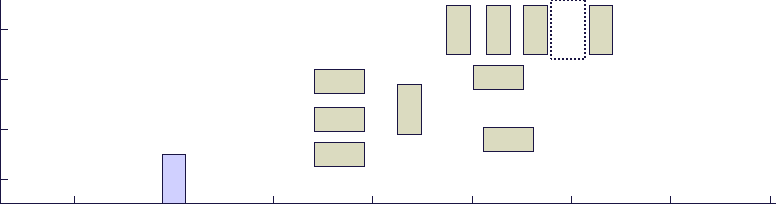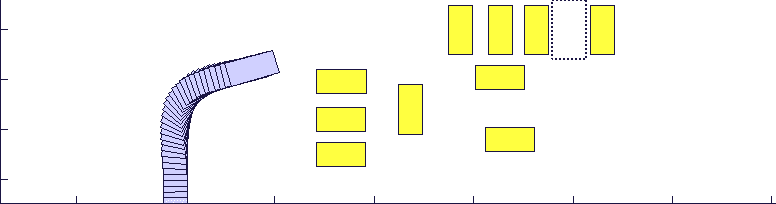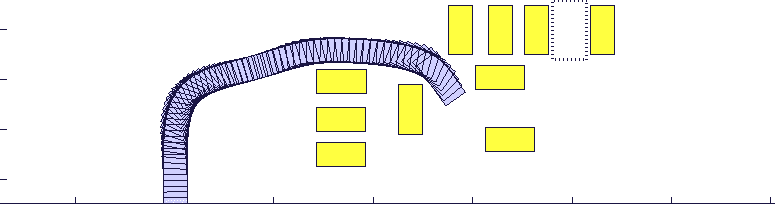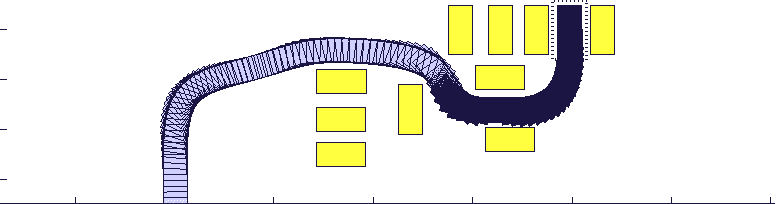
接下来是一个停车场的场景仿真,无人车需要绕开车辆和行人然后停入指定车位:
图五:停车库场景。其中黄色方块代表行人,蓝色虚线框为指定停车位,蓝色实线为参考路径。无人车需要绕开车辆行人停入车位中。
除了仿真以外,我们还在真车中实现了该算法,并应用于上述类似场景。超车场景:
















.jpg)