Barra权益类风险模型--Intelligent technology investment network-上海优钧机械设备科技

News Message

Barra权益类风险模型

by wittx 2020-09-05

Barra权益类风险模型

链接：https://www.zhihu.com/question/29355263/answer/577546758

从本质上说，特异性收益率应该没有什么时序和截面相关性，也不应该有什么所谓的“先验”，用足够长的样本时间序列计算独立每个股票算就行了。如果上面的假设都成立，那么这算出来的就应该挺好。Barra 的这几个修正都是针对这几个假设逐一不成立时的改进：
假设时序上不独立，为了解决它采用了 Newey-West 调整。
有的股票没有足够的历史数据（比如新股或者停牌了很久的），所以想了一个所谓的 structural 的方法。
预测出来之后，发现样本外不够准，有固有的 bias，所以在前两步的基础上进行了贝叶斯收缩，这是为了解决样本内、外的问题。
观察到特异性收益率在截面上可能出现同时被高估或者被低估的情况，造成样本外不准（因为波动率也是有聚类），所以进行了最后的 volatility regime adjustment。
可以看到，Barra 对 specific risk 建模的四步走是从解决一个又一个问题出发的，目标是尽可能的让样本外的预测更准确一些。这个思路本身是值得学习和借鉴的。在 A 股中做实证研究可以从实际数据出发，看看它的残差收益率到底有哪些特性、不满足哪些假设，从而借鉴上面的方法（当然也可以有别的方法）来修正，这是最终的目的。
最后，上面四步中，我之前对第三步的贝叶斯收缩写过一些介绍，也一并附在下面吧。
贝叶斯收缩是一个常见的将先验和样本估计值结合起来的手段；它是先验和样本估计值的线性组合（见《收益率预测的贝叶斯收缩》）。来看 Barra 的问题。首先根据实际数据计算出个股的特异性波动率。但是，Barra 指出使用样本内数据计算出的特异性波动率在样本外的持续性很差。
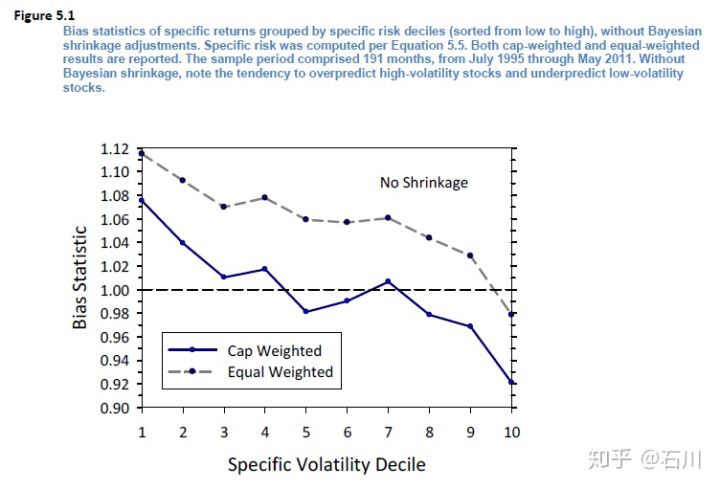
下图中，所有股票按照特异性波动率大小分成 10 档（图中第 1 档代表波动率最小；第 10 档代表波动率最大），计算每档的平均 Bias statistic（关于 bias statistic 的介绍可见本文第二节）。可以看到，对于波动率小的档，Bias statistic 显著大于 1，说明它低估了样本外这些股票的特异性波动率；而对于波动率大的档，Bias statistic 显著小于 1，说明它高估了这些股票在样本外的特异性波动率。
既然使用样本数据得到的 specific volatility 不准，那就需要使用先验来矫正一下。先验就是我们认为正确的特异性波动率，所以我们把样本数据计算出来的特异性波动率向着先验来靠拢，这就是“收缩”一词的意思，这就是为什么这个技术较贝叶斯收缩。
如何计算先验呢？对于任意给定的个股，Barra 采用一大堆个股特异性收益的波动率的均值作为先验。这个“一大堆”是什么呢？Barra 把所有个股按照市值分成十档，然后找到我们目标个股所在的市值那一档，而这一档中的所有股票就是这“一大堆”。
计算这一大堆中所有股票的特异性波动率，取它们的平均。怎么取呢？不是简单的等权，而是按照市值加权的。这个使用和目标股票处在同一市值这一档所有股票（一大堆）按照市值权重计算出来的特异性波动率就是先验。以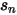表示市值档位 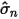$\hat σ_n$ 表示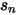中股票 n 的特异性收益率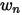，表示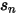中股票 n 的按照其市值计算出来的权重。则这个先验的表达式为：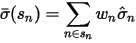
$\bar\sigma(s_n)=\displaystyle\sum_{n\in s_n}w_n\hat \sigma_n$
可见，先验就是把属于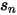内的所有股票的特异性波动率按照它们的市值为权重平均起来。
现在先验、样本观测数据都有了，最后一步就是把这二者线性组合在一起：
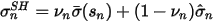
$\sigma_n^{SH}=\nu_n\bar \sigma(s_n)+(1-\nu_n)\hat \sigma_n$
上式中等式左侧就是收缩后股票 n 的最终特异性波动率，等式右侧的第一项中的 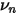$\nu_n$ 是在收缩时赋予先验的权重（称为收缩强度系数）。如何确定权重呢？它和样本估计值与先验的偏离程度有关。具体的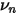， $\nu_n$ 的表达式为：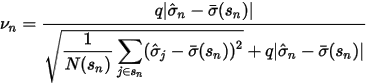
$\displaystyle\nu_n=\frac{q|\hat\sigma_n-\bar\sigma(s_n)|}{\displaystyle\sqrt{\frac{1}{N(s_n)}\sum_{j\in s_n}(\hat\sigma_j-\bar\sigma(s_n))^2}+q|\hat\sigma_n-\bar\sigma(s_n)|}$
上式中，q 是一个经验系数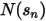，是市值档位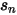中股票的个数。这个表达式中的分子以及分母中的第二项的 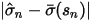$|\hat σ_n - \bar σ(s_n)|$ 表示了我们股票 n 的特异性波动率和其先验之间的偏离程度；而上式分母中的第一项是市值档位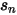中所有股票的特异性波动率和其先验偏离程度的标准差，它是这一大堆股票的平均偏离程度的一个度量。
最终的压缩权重 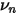$\nu_n$ 就由这两个偏离程度（以及经验系数 q）决定：
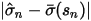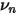$|\hat σ_n - \bar σ(s_n)|$ 越大， $\nu_n$ 就越大，而不要忘记 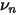$\nu_n$ 是先验的权重。这就是说，对于目标个股，样本数据计算的 specific volatility 越不靠谱（它的偏离程度和所有小伙伴的平均偏离程度相比更高），我们越不能相信它，而是越要相信先验，所以 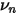$\nu_n$ 越大。
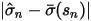$|\hat σ_n - \bar σ(s_n)|$ 越小，说明这个目标股票特异性波动率的偏离程度低，我们愿意相信它，所以这时赋予先验的权重 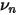$\nu_n$ 就要小点。
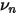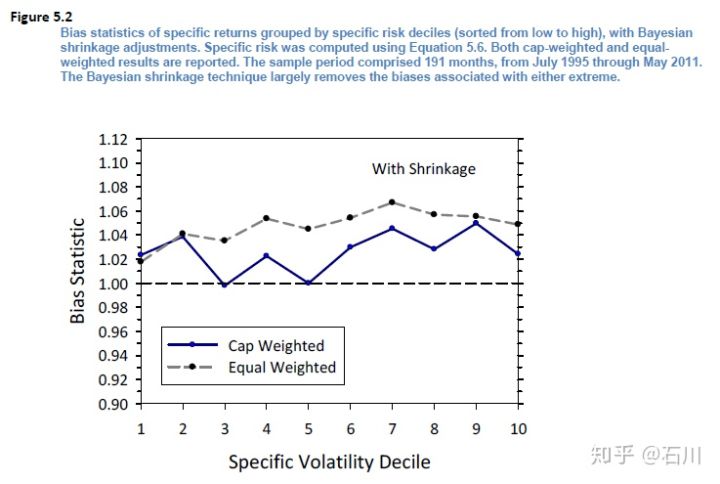
在上面 $\nu_n$ 的表达式中，唯一剩下的就是要确定经验系数 q 了。Barra 没有具体说，但是不难想它一定和 Bias Statistic 有关。贝叶斯收缩的目的就是为了降低个股特异性波动率的 Bias Statistic，所以可以通过综合考虑所有个股特异性波动率收缩前后 Bias statistic 的改进来找到合适的 q 值。
根据 USE4 文档中报告的结果，贝叶斯收缩效果显著改善了各市值档位内个股的特异性波动率（下图）。
以上就是对 specific volatility 做的贝叶斯收缩。

Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=137

©2021 上海优钧机械设备科技有限公司

Best Last Month

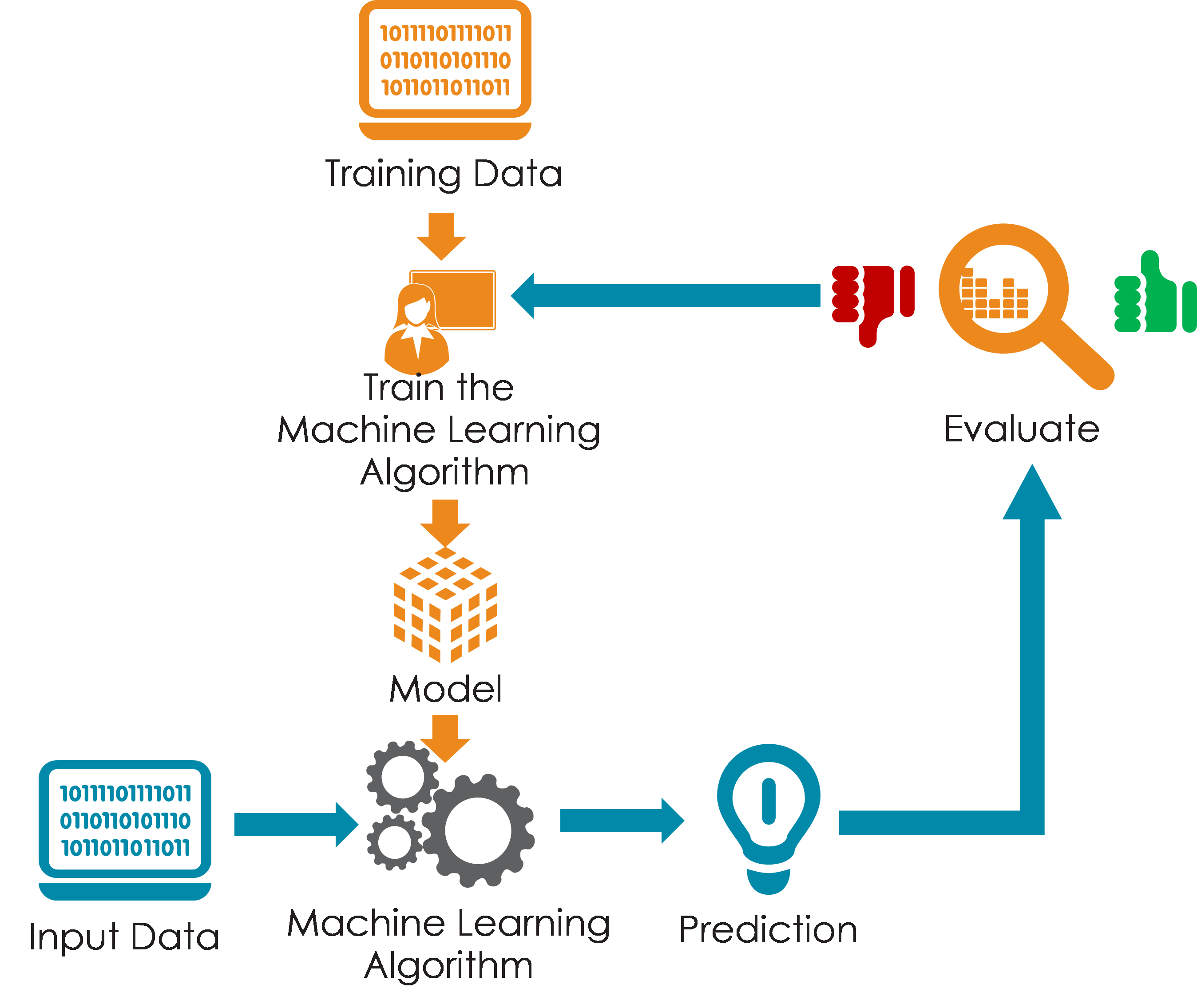
A Data-Driven Automatic Design Method for Electric Machines Based on Reinforcement Learning and Evol

A Data-Driven Automatic Design Method for Electric Machines Based on Reinforcement Learning and Evol
Information industry

by wittx

TCL科技：拟28亿元收购茂佳国际100%股权

TCL科技：拟28亿元收购茂佳国际100%股权
Information industry

by wittx

美股回落欧洲天然气暴涨

美股回落欧洲天然气暴涨
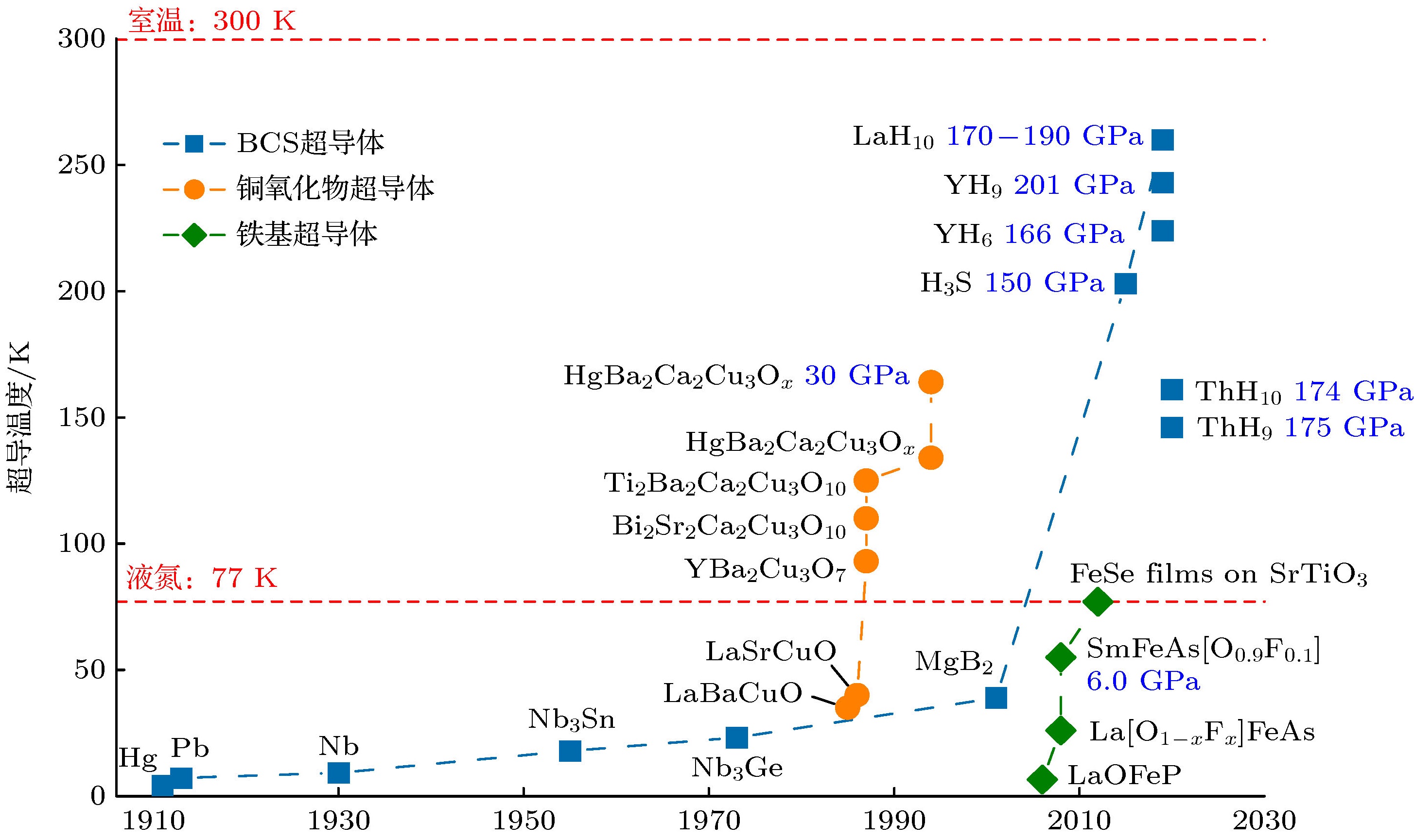
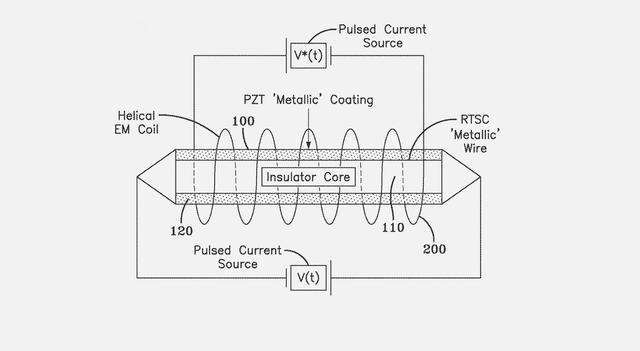
Information industry

by wittx

Superconductor Pb10-xCux(PO4)6O showing levitation at room temperature and atmospheric pressure

Superconductor Pb10-xCux(PO4)6O showing levitation at room temperature and atmospheric pressure
Information industry

by wittx

常温超导体专利

常温超导体专利
Information industry

by wittx

心率传感器原理

心率传感器原理
Information industry

by wittx

网络通信协议

网络通信协议
Computer software and hardware

by wittx

PLC基本控制线路与梯形图

PLC基本控制线路与梯形图
Information industry

by wittx

2020/12/15 金融行情

2020/12/15 金融行情
Information industry

by wittx

最新神经网络架构搜索 NAS 综述

最新神经网络架构搜索 NAS 综述
Information industry

by wittx