- Investment
- 科学论坛
- Program
- Recruitment
- Center
20世纪60年代初开始，以夏普(w．Sharpe，1964)，林特纳(J．Lintner，1965)和莫辛(J．Mossin，1966)为代表的一些经济学家开始从实证的角度出发，探索证券投资的现实，即马科维茨的理论在现实中的应用能否得到简化?如果投资者都采用马科维茨资产组合理论选择最优资产组合，那么资产的均衡价格将如何在收益与风险的权衡中形成?或者说，在市场均衡状态下，资产的价格如何依风险而确定?
这些学者的研究直接导致了资本资产定价模型(capital asset pricing model，CAPM)的产生。作为基于风险资产期望收益均衡基础上的预测模型之一，CAPM阐述了在投资者都采用马科维茨的理论进行投资管理的条件下市场均衡状态的形成，把资产的预期收益与预期风险之间的理论关系用一个简单的线性关系表达出来了，即认为一个资产的预期收益率与衡量该资产风险的一个尺度β值之间存在正相关关系。应该说，作为一种阐述风险资产均衡价格决定的理论，单一指数模型，或以之为基础的CAPM不仅大大简化了投资组合选择的运算过程，使马科维茨的投资组合选择理论朝现实世界的应用迈进了一大步，而且也使得证券理论从以往的定性分析转入定量分析，从规范性转入实证性，进而对证券投资的理论研究和实际操作，甚至整个金融理论与实践的发展都产生了巨大影响，成为现代金融学的理论基础。
假设持有某公司股票i的权重为w，s&p500指数股票组合m的权重为1-w，回报率为
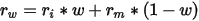
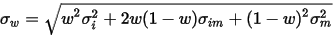
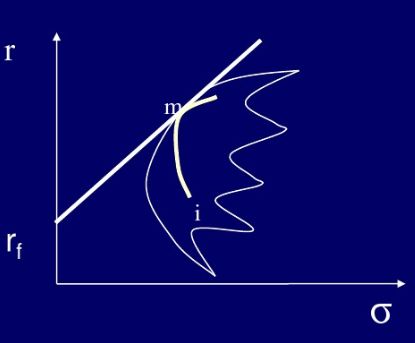
证券i和m构成的有效边界为im，im不可能穿越资本市场线，当w=0，im的斜率等于资本市场线的斜率
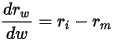
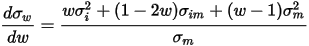
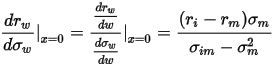
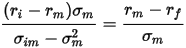
解得
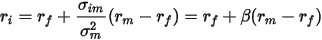
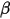系数是用以度量一项资产系统风险的指针，是用来衡量一种证券或一个投资组合相对总体市场的波动性（volatility）的一种风险评估工具。也就是说，如果一个股票的价格和市场的价格波动性是一致的，那么这个股票的Beta值就是1。如果一个股票的Beta是1.5，就意味着当市场上升10%时，该股票价格则上升15%；而市场下降10%时，股票的价格亦会下降15%。
当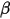 
值处于较高位置时，投资者便会因为股份的风险高，而会相应提升股票的预期回报率。举个例子，如果一个股票的Beta值是2.0，无风险回报率是3%，市场回报率(Market Return)是7%，那么市场溢价(Equity Market Premium) 就是4%（7%-3%），股票风险溢价(Risk Premium)为8% （2X4%，用Beta值乘市场溢价），那么股票的预期回报率则为11%（8%+3%， 即股票的风险溢价加上无风险回报率）。
以上的例子说明，一个风险投资者需要得到的溢价可以通过CAPM计算出来。换句话说,我们可通过CAPM来知道当前股票的价格是否与其回报相吻合。
CAPM与系统风险
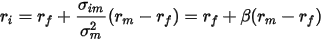
用统计公式表示为
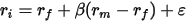
股票i和s&p500股票的组合收益的协方差为
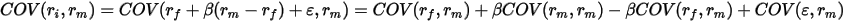
由于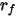 
为恒量， 
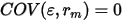，有
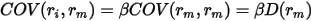
方差为
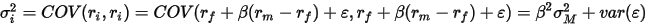
风险由2部分组成
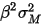整个市场的系统风险
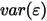不同公司的特有风险
通过组合投资，根据大数定律，可以消除特有风险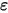 
，但市场的系统风险无法通过组合投资来消除。
CAPM的应用
假设一项资产的现价为p，以后的价格为q，则有
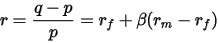
得到
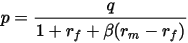
看一道例题：A公司明年股息0.5元，股息增速每年10%，当前无风险收益率3%，股票市场组合投资收益率11%，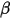 
值1.5，A公司目前合理股价是？
根据CAPM，A公司的必要收益率为
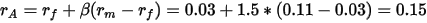
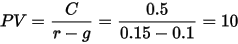元
