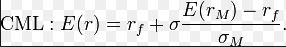- Investment
- 科学论坛
-
Program
- Recruitment
- Center
News Message
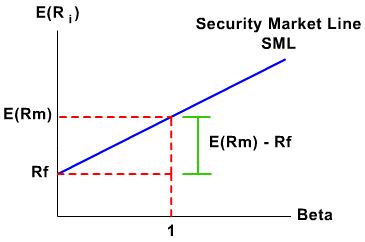
CAL CML SML
- by wittx 2020-09-04
链接:https://www.zhihu.com/question/22512309/answer/34008770CML:
作为一个理性投资者我们在投资的时候,最关心的就只有两件事:
第一:收益率(我投资100块钱,回报是多少)
第二:风险(我在得到这些回报的时候要承担多大的风险)这么看CML就很有用,因为这个模型就说了两件事,收益率和风险。多么贴心的模型~~~
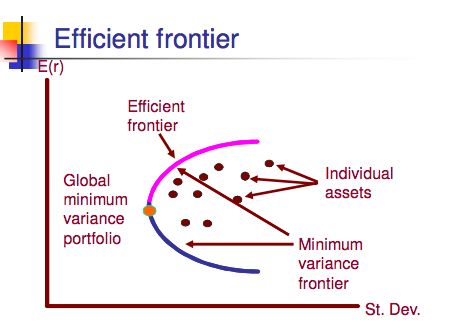
说CML 前先说说Efficient frontier, 也叫Markowitz Efficient frontier为什么叫Efficient frontier呢?
请看图,这个图里包含了看的到的10个风险资产(这里我们还没有考虑无风险资产),也可以简单粗暴的理解为10支股票,与在粉色线上的风险资产(虽然没看到具体"点"但粉色上是有股票的,相信我拉)基本上我们分析股票风险与预期回报率的时候,把股票数据输入EXCEL, Excel 就能根据你给出的一堆股票风险与收益画出这么一个线。好了,现在问题来了,给你这么一条线该如何选股票?
看到这十个小红点,你会选吗?
回答:当然不会啊,横坐标是风险,一样的风险粉色线上的点收益率更高啊!风险一样,当然选收益高的。多么狡猾的粉线,无论你在线下选哪一个点,一样的风险,粉线上的股票预期收益率总是最高的(最有效/efficient的)看到悲催的蓝线了吗?请问你会选蓝线上的股票吗?
必然不会嘛。同理,一样的风险干嘛不选收益率高的呀T_T 所以这条蓝线就这么被砍了~~~
当然不会有投资组合会出现在粉线以上。Global minimum variance profolio(全球最小方差组合)好高大上的名字
这个点很有意思,这个点回答的问题是:我想在风险市场里(比如股票市场,这样直观点)承受最小的风险时,所能获得的最大预期收益是多少?所以这条线回答的都是很实际的问题。在茫茫风险资产中我们的小粉线腾空出世了~~~~这条粉线的牛叉之处就是,无论你是风险厌恶投资者,还是风险中性,还是风险喜好的投资者,这条线上的风险资产(股票)总是最优的,理由是分析时候压根没考虑投资人的喜好,只是用风险资产(比如股票数据)分析得出。
这条线可以帮我们准确定位,在风险市场里(比如股票市场),我可以承担一定风险(比如10%的风险),我可以获得的最大预期收益率是多少?
至于有些追求高风险低回报的投资者(被砍的小蓝线是他们最好的选择),在这里我们就不要提了吧,土豪的世界我们永远不懂~
这时候要把无风险资产引入了,这也是最符合现实生活的版本,因为我们普通人可以选择要么把钱放在银行里睡觉(无风险投资)要么拿去买点股票或者基金(风险投资)进行风险投资。
然后你要想了,我到底应该把多少钱放到银行,多少钱拿去投资才能最大化预期收益呢?(换矫情的话说:风险和预期收益率如何组合才能达到最大回报率呢?)
CML 就可以帮助解决这个问题银行无风险利率是一定的(当然浮动,我们假设它一定)
CAL:
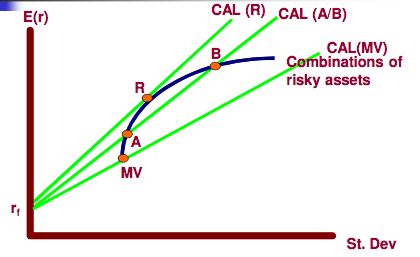
这里要引入CAL(capital allocation line) 线如其名,就是资产分配线,也是我们关心的问题:如果我可以把一部分钱放到银行一部分钱放到股票,我还可以承担一定风险时,这时候我可以获得的最大预期收益率是多少?(什么?为啥不全放银行,因为银行收益率只有4%,收益率不够买肾6啊)如果我可以多承担点风险,我的收益率又可以增加多少呢?(这个问题很实际的吧)
图里面一共有三条线,理论上说CAL有无数条,每一个相应的风险资产(每一只股票)与无风险资产都可以这么画一条CAL(比如:我可以把钱放银行,可以买阿里巴巴(一条CAL) ;我可以放银行,买苹果股票(又一条CAL).....所以这个组合理论上说是无数条,线上也不一定只有一支股票)。
看图:当有两点A,B 的时候,这时组合不是最优。
我怎么知道呢?中学数学告诉我们什么了?找最大、最小值,要找切点!(如果把公式放到这里,然后取点一代入结果很直观,我相信大家懂我的意思)开始画线了!从无利率风险出发,与资产风险组合(之前的小粉线)只有当相切(R)的时候才为最优。而这时我们的CML 就出现了~~~~~~有R的那条CAL 就叫CML。可以理解为CML是特殊形式的CAL,也就是我们最优的组合找到了!
换句话说,当我们假设可以以无风险利率来借钱投资的时候,我们“新的有效边界”出现了,并且这条新的有效边界是一条直线(之前的小粉是弯的,新的有效边界是直的)。从无风险利率出发,与之前的有效边界相切的那条直线,就是新的有效边界CML。而投资者这次是在这条直线上做风险与收益权衡。(我该存多少钱在银行,多少钱投资呢?如果我可以银行利率跟我妈借点钱,我该怎么去买股票/投资才能保证我可以承担最小的风险但可以获得最大的收益呢?)
这条CML对所有的投资者都是一样的!!这不是以个别投资者的喜好画出的线,而是给出一堆股票, 就可以客观画一条Efficient frontier line,再知道无风险利率,这条切线/CML(新的有效边界)是一定的,也是最有效的市场组合线。至少是数学模型上的最有效的。
至于对于个别投资者,你是想把更多的钱放到银行里睡觉,还是要问银行(我妈)借钱去投资股票那就是你们的事情了,CML 只能帮你们到这了。
(事实上投资者往往不会选择R,因为有的投资者会选择借钱去投资,预期回报率当然要大,但是相应的要承担更多的风险,也有投资者选择把更多的钱放在银行,少投资,当然承担的风险更小,相应的预期回报会更小。again,CML只能帮大家到这了。)
第一步:分析风险市场(比如:股票市场)的风险与收益率我们找到了小粉,
总结CML:
第二步:CAL就是进一步考虑投资问题了,帮我们知道,在考虑无风险投资的情况下(可以把钱放到银行里)我的投资预期回报率和风险之间的关系。我想要更大收益(至少大于存银行里的收益率)我需要额外承担多少风险。- CML 是帮投资者在茫茫股票中找到最优的投资组合。
- CML横轴是总风险,这里是包含了系统风险与非系统风险。我们当年就是要简单粗暴的想知道风险与预期回报的关系。(我们找小粉线时是简单粗暴的用股票的收益率与股票的风险。而股票风险是由股票价格波动率而得出,这里单个股票的价格既包含了这支股票所面临的系统风险(比如经济大环境波动率,通胀率等)也包含了这支股票的非系统风险(这支股票价格也包含了单个公司的公司风险,比如CEO绯闻拉,公司包子不好卖了等风险),也可以说股票的价格反应了股票所面临的所有风险)。
- CML一系列的衍生品所要给出的都是:到底哪个投资组合的总风险与回报最优(再一次!因为CML就只关心总风险与回报率的问题)
- 比如CML的斜率sharp ratio,sharp ratio越大(坡度越陡)预期回报率就越大(换句话说:考虑总风险与回报,sharp ratio越大预期回报率越高)。也就是我们要的最优的回报率。
- CML 是数学模型上的最优。为什么这么说,模型里的R在理论上是最优的投资组合,也就是数学上来说这个组合是风险与回报率结合的最好的投资组合。但是我奶只要把钱放到股票里连睡觉都睡不着了,还不停的折磨这我们一家人问股票涨没涨啊,跌没跌啊,波动一点都块要我奶命了~~这个时候不得不说,钱放到银行里对大家都是最好的(每个人的Utility/效用函数是不同的,对风险敏感程度也不同)。如果想象成相亲的话,CML是媒婆,它只负责匹配两个人物质条件般配不般配,两个人是不是最优组合,至于有没有爱情啥的,CML这个媒婆都不负责的。
- R 是一个神奇的点,这个点必须包含所有可能的风险投资资产,假设王思聪家的股票没有包含在这个风险投资组合中,这样就会变成没有人买他家股票,于是王思聪家股票便宜到1块钱1股,然后股票预期回报会增加,这样他家股票又变成大家都想买的股票,重新闪亮回归R这个风险组合中。也就是“看不见的手”会根据供需关系来调节资产价格(这个R点大家知道是个投资组合,并且这个组合里有好多投资资产就好)
在网上找了个公式截图:
来添坑~~~
为什么这么久才来填坑呢,因为我就是要大家完全忘记SML这回事。问SML和CAL, CML有什么关系,答案就是没特别大的关系,就有那么八竿子挨了一丢丢的关系~~~~SML是完全另外一个故事。
CML 与 SML 区别一:用途不一样
当大家开心的知道了CML的时候,以为自己已经掌握了投资大法,眼看就要登上人生巅峰迎娶白富美的时候,一个非常关键的问题出来了~~
请问你根据什么去知道你的预期回报是否合理呢?
什么?没听懂?
换个问法~~~我请问你,你怎么知道王思聪家股票5毛一股就是合理的价钱呢?
国民老公家股票就可以漫天要价5毛一股?!我要出手买了亏了算谁的?CML解决了要把多少钱买股票,多少钱放银行。但是股票在什么价格上买才是一个合适的价格?换句话说,我咋能给股票定个合理价格呢?作为一个投资者,可以给一个投资产品合理的估价是非常重要的,如果谁可以鼓捣出一个准确的市场定价模型,就等于开了挂~~你想啊,你用这个模型掐指一算就知道明天苹果股票要多少钱,阿里巴巴多少钱,你今天就可以在市场还没反应过来的时候去赚钱。这个时候才能真正登上人生巅峰,迎娶白富美!想想就有点小激动呢~~学金融的也是俗人呐,大家当然是前仆后继,飞蛾扑火一样的去找这样的模型,光论文都堆的不知道几火车皮了~~~
SML就是由一个模型来的,模型的名字叫资本定价模型(capital asset pricing model)简称CAPM ~~直白不直白?!所以SML是关于资本怎么定价的故事,CML是说怎么权衡投资的故事,你说他俩是不是从用途上讲就不一样~~
图片来源网络(楼主不生产知识,楼主只是知识的搬运工)
现在我们开始建模型~~~CML与SML第二个不同:横坐标的风险不同
我想要给一个资产估价,我要想的第一个问题是,我这个东西要承担的风险是什么?我必须要根据这个东西承担的风险然后再给合理定价。所以我最关心的是当总体经济变好,或者变坏时(例如股票大盘总体涨跌)我这个资产相对涨跌多少,也就是系统风险。
————————这里是废话,可以直接跳过看黑子总结————————
那我该不该关心非系统风险呢?换句话说,我该不该关心单个公司所面临的风险呢?比如:哪家包子铺的CEO诈骗了,哪家羊肉串老板家炉子丢了~~? 回答是:请不要在意这些细节!!!因为作为一个自由投资者,我可以买许多不同的资产去投资,我可以把一条街的包子铺的股票都买了,这家CEO诈骗被抓了,隔壁王老五家的包子就好卖了,股票这家跌,那家涨,对我来说也没啥损失。我把我们学校门口所有卖 羊肉串公司的股票都包了,这家炉子丢了,隔壁老李家羊肉串就好卖了,对我来说都没有特别大的影响。我知道拉,你一定要说,楼主等等,我哪有那么多钱把鱼塘都包下来啊,我又不是塘主!!我买不下所有的股票啊,你让我这么算不是坑我吗?!但是朋友~~~这个市场是面对所有投资者的,咱没钱都包下来,总有人(想象出那么一个人)有钱包下来不是~~咱们这时候必须要把自己当有钱人,站在宏观的角度去考虑问题,才能给一个资产合理定价~~~(关于这些假设我后面会说,埋个伏笔)咱们现在是跟着那些伟大的经济学家的脚步去考虑问题,请不要入戏太深,总是关注自己兜里的仨瓜俩枣。
————————————————————————————————————所以作为一个理性投资者,不同风险资产是互相独立存在,在足够大的投资组合中,个体风险会被分散近似为0,所以我们不应该关心非系统风险(个别公司风险),而是该关心系统风险补偿(无法由大量投资抵消的风险)
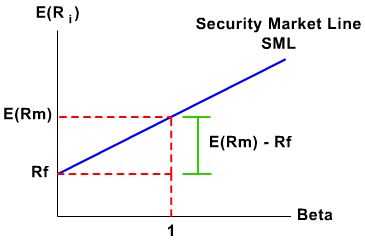
所以看图,横轴这时候是 Beta代表的是系统风险(无法通过大量投资而分散的风险)
但是在CML里横坐标是包含了系统风险与非系统风险这种区别本质是,两条线的用途不同,所以关注的风险也不同。
搞清楚横轴,我需要什么风险被补偿,一切都好办了。所谓定价也就是找到合理的回报率。比如我知道苹果股价现在100。我估计呢,苹果股票实际值110。这个110是我估计的,我估计得准了,100的时候买进,当升到110时我卖掉,10块钱的回报就是我赚的,10% 的回报率是我当年根据模型估计出来的。
好了,我们现在开始估计预期回报率了。
咱主要看两点:第一:这个风险资产回报率是高于银行无风险利率(股票回报率一定是要高于银行无风险利率的回报率投资者才要投资是吧。要是股票回报率低于银行利率,我岂不是拿着买白菜的工资操着卖白粉的心?!)所以咱们这条SML的起点是银行无风险利率。
第二:我的这个预期回报率要加上系统风险价格补偿。也就是系统风险回报率或者市场回报率。
公式大模样有了:
我的预期回报率=银行无风险利率+ 系统风险回报率这里出现了CML与SML的第一个相同点:都和无风险利率有一腿
- CML和无风险利率有一腿是因为我可以存钱在银行这里涉及到银行的无风险利率,或者投资资金来源假设可以以银行无风险利率借入钱(其实这个假设有点扯,这年头除了问我妈借钱能以银行无风险利率还,恐怕自己男朋友都没这个交情了 )
- SML和无风险利率有一腿是因为,我对一个风险资产估价的时候,这个风险资产的回报率是应该由两部分组成:第一,无风险利率;第二:在无风险利率的基础上再加上我需要承担额外系统风险那块的额外回报率。
还是那句话,虽然两个模型都有无风险利率,看起来是一个共同点。但由于模型的用途不同,我们考虑的角度不同,所以尽管是一样的无风险利率,但这背后为什么要用这个无风险利率的解释也是不同的
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=111
wittx

Best Last Month
.jpg)
Information industry by wittx

Information industry by wittx
Information industry by wittx
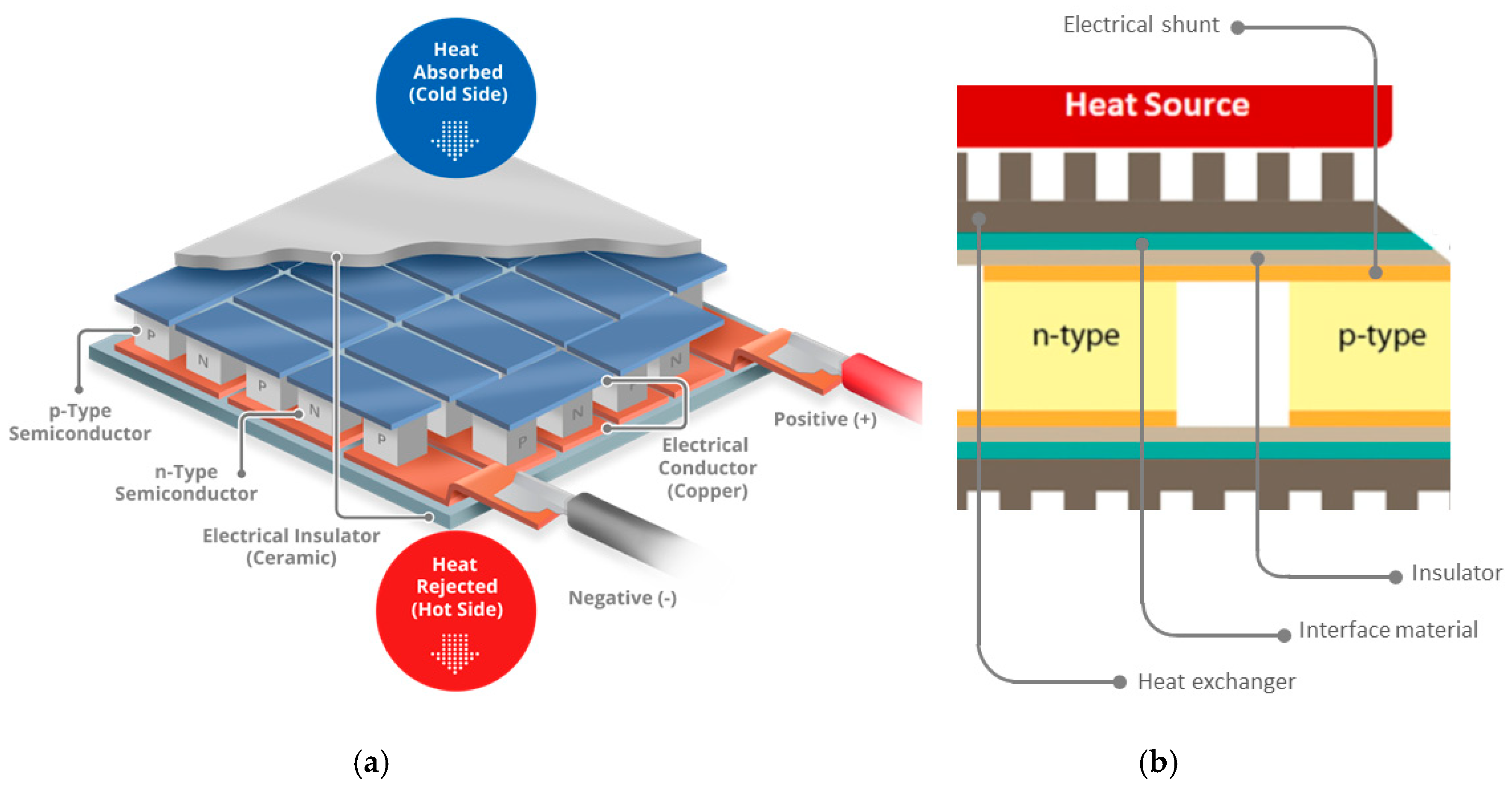
Information industry by wittxImproved thermoelectric power factor and conversion efficiency of perovskite barium stannate
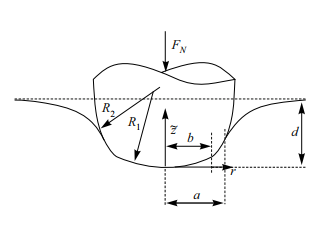
Information industry by wittx
Information industry by wittx
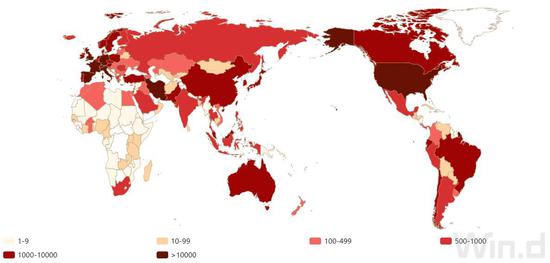
Information industry by wittx

Information industry by wittx

Information industry by wittx

Information industry by wittx