-
News Message
二叉树 B+Tree
- by wittx 2022-11-22
常见数据结构
常见的查找数据结构包括HASH表和二叉树（红黑树）。
Hash表介绍
Hash表是普通数组的一个扩展，它支持O(1)的操作，包括查询，插入，以及删除。但是Hash支持O (1)时，是一个比较理想的状态，要求很好的Hash函数以及比较多的冗余内存。这部分咱们暂时不展开。
二叉树介绍
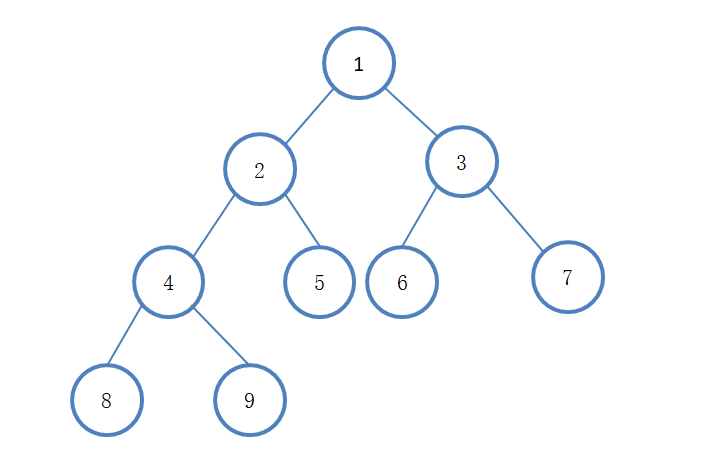
二叉树是另一种比较经典的查找数据结构，其特点如下：
- 只有一个根结点
- 任何一个子节点最多允许两个子节点
- 左子节点的值小于父节点的值，右子节点的值大于父节点的值
一个典型的二叉树如图所示:
虽然Hash表或者二叉树是比较常见的查找数据结构，但是大部分数据库存储引擎并不使用它们作为主要的数据结构（也有例外的），而是使用B-Tree以及B-Tree的变种B+Tree。
提问：有哪些数据库存储引擎是使用Hash表或者二叉树作为主要的数据结构，为什么它们使用这些数据结构？
B-Tree树
B-Tree和二叉树类似，有如下特性：
- 只有一个根节点
- 一个节点允许最多有N个值，N＞2，有N+1个字节点
- 节点中值按照从小到大的顺序排列
- 第m个子节点中的所有值小于第m个值，第N+1个子节点的所有值大于第N个值
- 叶子节点没有子节点，所有叶子节点到根节点高度一样
- 一般除了根节点，节点值的个数大于等于N/2
下图为一个N=4的B-Tree：
B-Tree优势
大多数数据库存储引擎使用B-Tree的原因有两个：
- 数据库存储最终需要从文件系统中读取这些节点的数据，而从文件中读取节点操作是比较耗时，因此需要一次尽量多读取一些数据，B-Tree支持N个值，正好可以用来减少文件读取的次数。例如：某个B-Tree的N为128（2^7），从2^14中读取一个数据，平均需要读取2次文件（第一次读取根节点，第二次读取叶子节点）；而，如果使用二叉树，则平均需要读取14次文件（第一次读取根节点，最后一次读取叶子节点）。
- 硬盘有一个特性，就是硬盘读写数据时，是一个数据块一个数据块的读写，不是内存中那样，一个字节一个字节的读写。如果从文件中读取的字节较少，其实依然是先一个数据块一个数据块的读取，然后裁剪，这样就会造成很多读取的数据是无效的，浪费了时间和存储空间。
在数据库存储引擎中，最常使用的是B-Tree的变种：B+Tree。B+Tree除了有B-Tree所有的特性，还有另外几个特性：
- 叶子节点包括了所有的值（叶子节点中的值，可能在其他节点中也存在），所有值到根节点的高度是一样的
- 叶子节点有一个指向其右边叶子节点的“指针”(这样便于范围查询)
- 第m个子节点的值都小于或者等于父节点中的第m个值
下图为一个N为4的B+Tree：
B+Tree的操作
B+Tree一般至少提供三种操作：查询，插入以及删B+Tree查询过程：
- 根节点开始查询，然后层级下降直到叶子节点；
- 每个节点的查询流程如下：
- 查询的key值和节点中的第i个值比较，如果小于等于第i个值，下降到第i个子节点；然后在子节点中重复节点查询流程；
- 如果查询的key值大于节点中所有的值，下降到第n+1个子节点；然后在子节点中重复节点查询流程；
- 叶子节点中，查询的key值和节点中的第i个值比较，如果二者相同，返回对应的value；没有找到相同的值，则返回没有找到对应的value（查询的key在B+Tree不存在）
B+Tree插入
B+Tree的插入相对查询要复杂一些，插入要涉及两个新操作：分裂和增加新根节点。B+Tree的节点能够容纳的值是N，如果一旦超过N，一个节点就要分裂成两个节点；如果根节点分裂了，就需要创建一个新根节点。
B+Tree的插入操作：
- 新的key值插入到叶子节点上
- 查找叶子节点的是方式和B+Tree查询过一样；但是有不同，如果查找到的子节点，其值的个数为N，需要对该子节点进行分裂。
- 如果该子节点为根节点，需要创建一个新的根节点，子节点分裂两个节点，新的根节点作为两个子节点的父节点
- 非叶子节点分裂：第1个到N/2个的值以及第1个到N/2+1个子节点指针分配到第一个子节点；第N/2+2个到N个的值以及第N/2+2到N+1个子节点指针分配到第二子节点；第N/2+1个值插入分裂节点的父节点中，位置为分裂前节点的前一位，该位置的子节点指向第一个子节点。
- 叶子节点分裂：第1个到N/2个的值分配到第一个子节点；第N/2+1个到N个的值分配到第二子节点；第N/2个值插入分裂节点的父节点中，位置为分裂前节点的前一位，该位置的子节点指向第一个子节点。
- 找到对应的叶子节点以后，根据key值的大小，插入相应的位置（节点中的值按照大小顺序排列）。
叶子节点插入流程
非叶子节点插入流程
B+Tree删除
B+Tree删除是所有操作中最复杂的。除了需要考虑到节点合并以及根节点删除的操作，还需要考虑到删除操作带来的连续合并操作和邻近节点寻找的过程。
B+Tree删除操作：
- key值直接从叶子节点上删除
- 查找叶子节点的是方式和B+Tree查询过一样
- 如果删除key值以后，其值的个数少于N/2，且该叶子节点不为根节点，需要对该叶子节点进行合并。
- 寻找到该叶子节点的邻近节点，选择一个值较少的邻近节点（一般会有两个邻近节点）
- 如果邻近节点值个数与该叶子节点值个数之和小于N，可以直接合并这两个节点
- 如果邻近节点值个数与该叶子节点值个数之和大于N，需要重新分配两个节点中的key值，使其拥有都大于N/2个值
- 如果合并叶子节点或者子节点时，出现节点合并，那么需要从父节点中删除其中一个值，这样可能导致父节点的值个数少于N/2，这样父节点也需要节点合并操作，从而引发连续节点合并操作，这样操作可以一层层往往上一层节点传递，最终达到根节点。
- 如果根节点只有一个值，其子节点出现了节点合并操作，就需要删除这个根节点，合并后的新节点为新的根节点。
节点合并
B+Tree节点一般值的个数不少于N/2，所以如果碰到某个节点的值个数少于N/2，需要合并邻近节点。但是，邻近节点值的个数大于N/2，就可能出现合并后节点的值个数大于N。
叶子节点合并操作流程
叶子节点内容调整流程
寻找邻近节点
寻找邻近节点是节点合并的前置操作，需要先找到邻近节点，才能让邻近节点和当前节点进行合并操作。但是有时候邻近节点和当前节点有时候并不拥有同一个父节点，这个时候会极大影响后面的节点合并操作，比如：节点发生合并后，如何从父节点中删除一个值？节点内容调整，如何调整父节点中的值。
下面是邻近节点和当前节点不共享父节点的情况：
父节点中删除一个值，需要调整两个节点中的父节点内容，涉及的节点就比较多。由于这个例子中，两个节点的父节点共享父节点，涉及的节点较少；如果是父父父节点才相同，涉及的节点就会更多，更难处理。为了处理这个问题，我们先定义一个最佳邻近节点：拥有相同父节点中，值个数最小的邻近节点为最佳邻近节点。
选择最佳邻近节点合并操作：
删除根节点
如果根节点恰好只有两个子节点，而这两个子节点发生了合并，这个需要删除旧的根节点，合并后的节点为新的根节点。
连续合并操作
删除不但会引起叶子节点的合并，也会引起其他节点合并。叶子节点合并了，会从其父节点中删除一个值，这样就可能会引发父节点的合并，而父节点删除又有可能导致父父节点的删除，从而引发父父节点的合并……，以此类推，一直删除到跟节点。
删除叶子节点值
合并叶子节点
删除父节点
合并父节点以及删除父父节点
合并非叶子节点
合并非叶子节点可以认为是分裂非叶子节点的“逆操作”，分裂时，需要从分裂后的第一个节点中取出一个值插入父节点；合并时，也需要从父节点从取出一个值放入合并的节点中。
总结
B+Tree的所有操作，过程都需要遵循B+Tree的基本特性，如：节点内的值按照大小顺序排列等。B+Tree所有操作都是O(logN)的时间复杂度，所以B+Tree操作很稳定，正因为如此B+Tree在传统关系型数据库中广泛使用。
提问：新兴非传统数据库会使用哪些数据结构？与B+Tree比起有什么优缺点？除了B+Tree还有哪些B-Tree的变种，它们有什么优缺点？
算法与实践
本文介绍了B+Tree的基本构造以及操作过程，但是按照这些描述比较难以实现一个内存版的B+Tree，这就是算法和实践的差异，实践中还需要考虑很多工程问题。正因为为了解决这些工程问题，真正实现的B+Tree需要根据不同的情况进行调整。
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=1037
Best Last Month
Information industry by wittx
Medical science by wittx
Information industry by wittx
Information industry by wittx
Mechanical electromechanical by wittx
Information industry by wittx
Information industry by wittx
Medical science by wittx
Electronic electrician by wittx
Information industry by wittx
