
- Investment
- 科学论坛
-
Program
- Recruitment
- Center
News Message
网络上的标签传播
- by wittx 2022-11-22
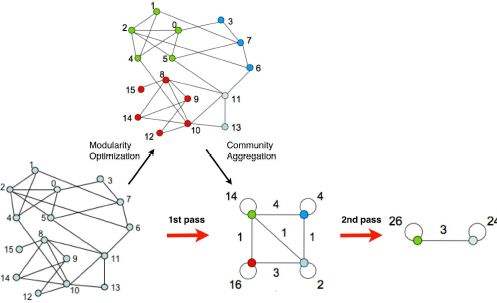
标签传播实际上应该叫Label Propagation Algorithm(LPA),之前还搞错了,嗨。
标签传播这个问题实际上属于semi-supervised,在部分数据已知,而另一部分数据未知的情况下,根据数据特征的相似或者有直接的结构联系去揣测未标注数据的标签。在标签传播中,主要框架是GCN这样的AXW形式的框架,然后修改loss和A。因而这次从3个文章开始介绍这个东西。
首先是Unifying Graph Convolutional Neural Networks and Label Propagation
https://arxiv.org/pdf/2002.06755.pdf
这个文章主要考虑了标签传播的两个层面,一个是特征的传播,一个是标签的传播,并且,这两种传播都是使用的这种很习惯的表示方法
这样的形式,如果考虑a使x平滑(GCN考虑的事情),则一般也会带有误差项epsilon,即
这样,就可以考虑L-Lipschitz 平滑方法,即|y1-y2|=| M(x1)- M(x2)|<=L||x1-x2||. M表达y为x的映射。这时,作者认为这个式子是可以再化为一个以epsilon为中心主导的估计误差:
这里L是一个常数。而我们希望这个epsilon项尽可能小,这样才能使得标签的误差小。在节点周围邻居少的情况或者节点本身特征稀疏的情况下,epsilon可能就会变得比较大,这样就违背了这个估计设立的背景了,所以作者使用了LPA的方法。注意这里的LPA并不是说这些节点一定要沿着图的边传播,而是认为这些节点如果类别相似就理所应当会有相近的信息。这些相近的信息被定义成intra-class,如图所示
因此,优化目标就是基于LPA的GCN传播。
LPA的目标为
GCN本身的设计为:
注意在GCN的更新中的A是来源于LPA的,和图本身似乎并没有关系。J是交叉熵损失函数,a为已标注的数据,m为数据的总量。
第二篇为来自CVPR的用标签传播做图像分类的:Label Propagation for Deep Semi-supervised Learning
https://arxiv.org/pdf/1904.04717.pdf
这篇文章引入了一个叫做伪标签的概念(pseudo-labeling)就是说我们认为一部分未标注的数据他拥有和已有数据一样的特性,所以在训练迭代时,这些未标注的数据可以一部分一部分的被标注上标签。因而在构建loss的时候,就需要从两个层面考虑了,一个是针对已有标签的loss,一个针对这种伪标签的loss。这里L表示有标注的数据,U表示无标注的数据。
所以,已有标签的loss为一个纯有监督的:
而无标签的loss则为:
作者考虑说这些传播的标签有可能存在数据不均衡问题,所以在这里对无标签部分的loss又做了一次修改
W是一个权重,z为预测的标签正则式,H是一个熵,c为类别总数,所以很容易发现w就是一个控制是否数据均衡的一个称。并且跟了一个针对每一个标签的权重的参数,定义为:
这样,这个模型的框架就变成了
中间的传播过程看上去很熟悉的样子,很像GCN的写法,只不过A是一个affinity matrix,而W才是真正用来传播的无向图。A的定义为:
之后,需要解一个方程
Alpha是一个可设置的参数,Y是一个n*c的全局矩阵标签,所以我们需要求解的是Z。虽然可以直接取逆矩阵直接算,但作者认为太费神了,所以用了共轭梯度下降来解这个方程(conjugate gradient(CG))。对于z这个方程的迭代式可以写做
第三篇是KGNN-SL,Knowledge-aware Graph Neural Networks with Label Smoothness Regularization for Recommender Systems
https://dl.acm.org/doi/pdf/10.1145/3292500.3330836
这个应该是比较著名的一个文章了,刚刚才发现作者和第一篇的作者是一个人,是个大佬。。。
这个文章主要是构建推荐系统的异质图,使用标签传播的方式去预判用户希望的商品。而这个图本身的节点包括商品和一些非商品项,这里的非商品项指的是商品本身的性质属性。这些商品本身的性质才是构成这个商品本身特性的核心。
这个图是针对一个用户u的,用户和商品之间存在一个评分
g是点乘,表示用户对这些属性关系的重视程度。在此基础上,用GCN的传播,
所以,这前几步看上去都是比较简单的,重心就落到了最后一步,怎样做这个标签平滑。
在这篇文章中,作者定义了一种能量来表示信息传递:
这个式子看上去就是laplacian的信息传递过程(搜瑞利熵能看到详细过程),但是a的定义不一样。而我们需要求解这个能量最小,即
对这个式子进行简化,最后可得出这个lu只和非商品的实体有关,具体推导就不写了,大题就是求导然后得极值然后反向带入。最后优化结果为
但是实际情况是我们一般是不能直接解出来的,所以作者使用了迭代的方法来解这个过程。这个迭代的过程分为两个步骤:
1. 对所有实体进行更新
2. 对商品项进行更新:
具体证明也不展开了,这个证明是证虽然我们这样更新看上去和直接更新lu没什么关系,但他确实是可以work的。主要采用的方法是分解子矩阵和证明迭代过多的时候某一项会趋近0.
最终,标签平滑的R项就变成了
Ps:这学期终于把课程上完了,选了一个把人折腾的半死不活的矩阵计算。好在上完以后发现看一些图网络的文章居然感觉没那么吃力了,也算事好事吧,看来这课还是有那么点用。。。
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=1035

Best Last Month

Information industry by wittx
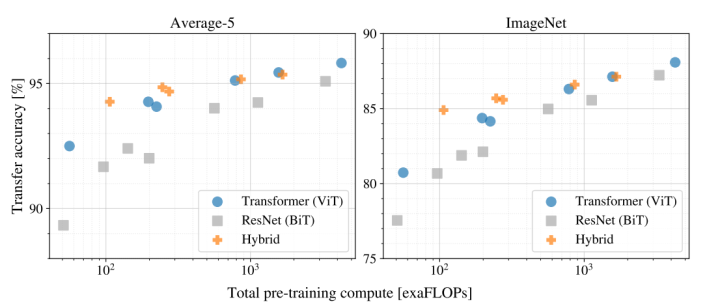
Information industry by wittx

Information industry by wittx

Information industry by wittx
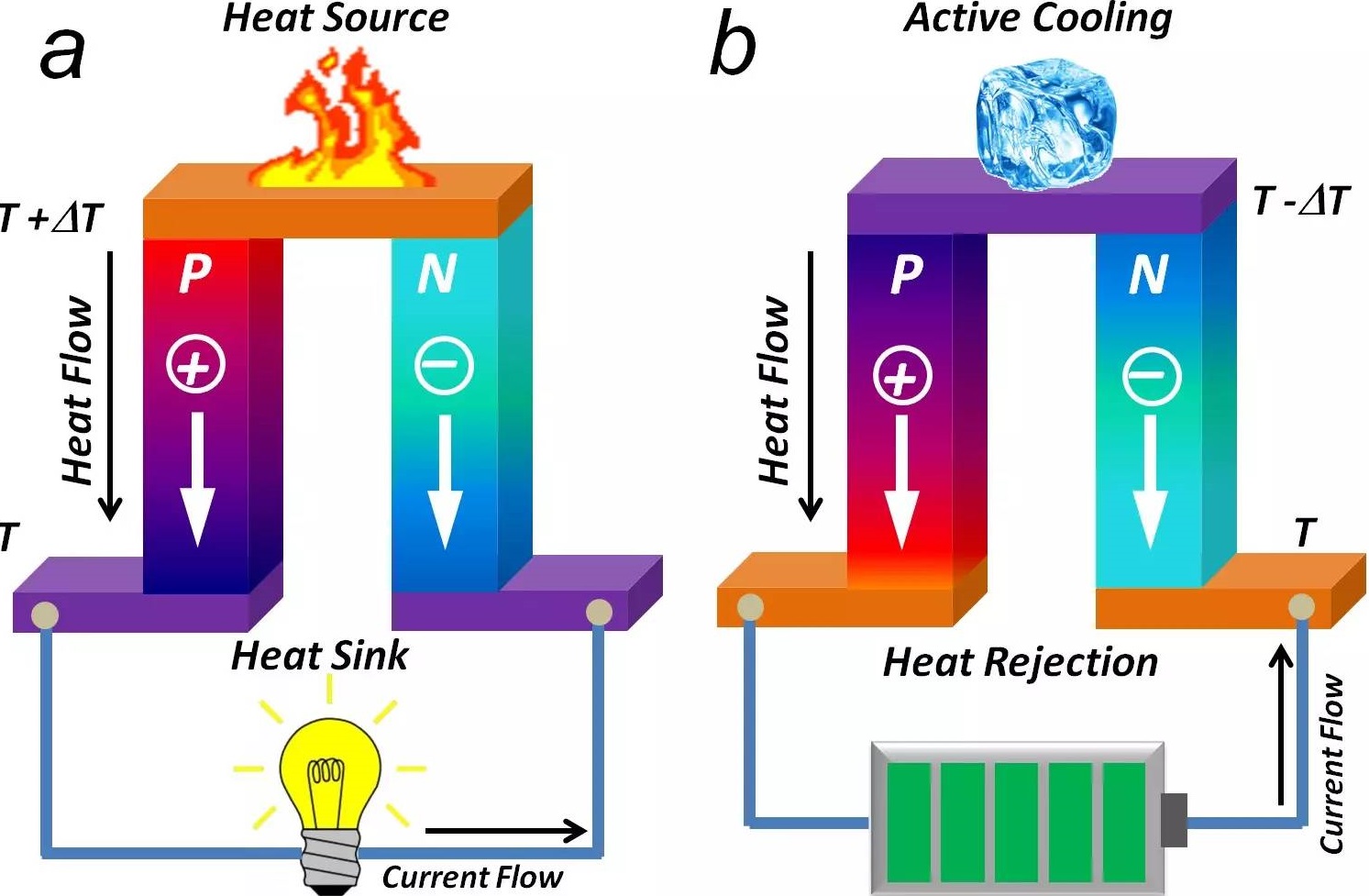
Information industry by wittxNature High-efficiency solar thermoelectric conversion enabled by movable charging of molten salts

Information industry by show

Information industry by wittx
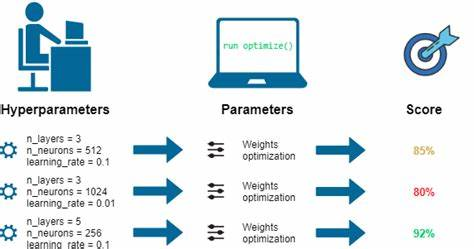
Information industry by wittxActor-Attention-Critic for Multi-Agent Reinforcement Learning

Information industry by wittx

Information industry by wittx


























